All AP Calculus BC Resources
Example Questions
Example Question #27 : Maclaurin Series
Example Question #51 : Polynomial Approximations And Series
Example Question #29 : Maclaurin Series
Example Question #30 : Maclaurin Series
Example Question #51 : Ap Calculus Bc
Example Question #52 : Ap Calculus Bc
Example Question #51 : Taylor Series
Example Question #1 : Maclaurin Series For Exponential And Trigonometric Functions
Write out the first three terms of the Taylor series about 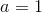
The Taylor series about x=a for a function is given by
For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
The derivatives were found using the following rules:

Now, using the above formula, write out the first three terms:
which simplified becomes
Example Question #311 : Series In Calculus
Find the Maclaurin Series of the function
up to the fifth degree.
The formula for an i-th degree Maclaurin Polynomial is
For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.
The summation becomes
And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial
Example Question #1 : Radius And Interval Of Convergence Of Power Series
Which of following intervals of convergence cannot exist?
For any 
![\small [a-\epsilon,a+\epsilon]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/380619/gif.latex)
For any 




Certified Tutor
All AP Calculus BC Resources












































![(1+e^1)+[(2+e^1)(x-1)]+(x-1)^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436356/gif.latex)
![0+(1+e^1)+[(2+e^1)(x-1)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436358/gif.latex)
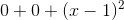
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436360/gif.latex)

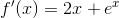


![\frac{(1+e^1)(x-1)^0}{0!}+\frac{[(2+e^1)(x-1)^1]}{1!}+\frac{(2+e^1)(x-1)^2}{2!}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436367/gif.latex)
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436368/gif.latex)
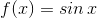


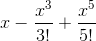







![\small [2,10000]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/380616/gif.latex)
![[q,p]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/380615/gif.latex)




