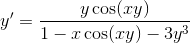Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Implicit differentiation

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #71 : Applications Of Derivatives

Differentiate the following implicit function:

(x-2)^2+y^2=121

Possible Answers:

$\frac{dy}{dx}=y^2+2x-4$

$\frac{dy}{dx}=x+y+2$

$\frac{dy}{dx}=\frac{2x-1}{y}$

$\frac{dy}{dx}=2x+2y+4$

$\frac{dy}{dx}=\frac{2-x}{y}$

Correct answer:

$\frac{dy}{dx}=\frac{2-x}{y}$

Explanation:

For this problem we are asked to find $\frac{dy}{dx}$ , or the rate of change in y with respect to x.

To do this we take the derivative of each variable and to differentiate between the two, we will write dx or dy after.

(x-2)^2+y^2=121

would then become

(2x-4)dx+(2y)dy=0

We note that the derivative of a constant is still zero.

We must now rewrite this function in the form $\frac{dy}{dx}$

(2y)dy=-(2x-4)dx

$\frac{dy}{dx}=\frac{-2x+4}{2y}$

$\frac{dy}{dx}=\frac{2-x}{y}$

Report an Error

Example Question #601 : Derivatives

Find the implicit derivative, $\frac{dy}{dx}$ a circle centered at (2,-1) with radius r=2 .

Possible Answers:

$\frac{dy}{dx}=\frac{x+2}{y-1}$

$\frac{dy}{dx}=2x+2y-1$

$\frac{dy}{dx}=-\frac{x+2}{y-1}$

$\frac{dy}{dx}=x+y-1$

$\frac{dy}{dx}=-\frac{x-2}{y+1}$

Correct answer:

$\frac{dy}{dx}=-\frac{x-2}{y+1}$

Explanation:

The equation of a circle centered at (2,-1) with radius r=2 is (x-2)^2+(y+1)^2=4 .

We first expand our equation to simplify the derivative.

x^2-4x+4+y^2+2y+1=0

x^2-4x+y^2+2y=-5

Take the derivatives of x and y we get:

(2x-4)dx+(2y+2)dy=0

Since the derivative of a constant is zero.

Next we must rewrite our equation in terms of $\frac{dy}{dx}$ :

(2y+2)dy=-(2x-4)dx

$\frac{dy}{dx}=-\frac{2x-4}{2y+2}$

Simplifying:

$\frac{dy}{dx}=-\frac{x-2}{y+1}$

Report an Error

Example Question #71 : Applications Of Derivatives

Given that y=y(x) , find the derivative of the function

$y=\sin(xy)+y^3$

Possible Answers:

$y'=\frac{y\cos(xy)}{1-x\sin(xy)-3y^2}$

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-3y^3}$

$y'=\frac{x\cos(xy)}{1-x\cos(xy)-3y^2}$

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-3y^2}$

Correct answer:

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-3y^2}$

Explanation:

To find the derivative with respect to y, we use implicit differentiation, which is an application of the chain rule.

$y=\sin(xy)+y^3$

$y'=\cos(xy)(y+xy')+3y^2y'$

$y'-xy'\cos(xy)-3y^2y'=y\cos(xy)$

$y'(1-x\cos(xy)-3y^2)=y\cos(xy)$

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-3y^2}$

Report an Error

Example Question #72 : Applications Of Derivatives

Given that y=y(x) , find the derivative of the function

$y=\tan(y^2)+xy^5$

Possible Answers:

$y'=\frac{y^5}{1-2y\sec^2(y^2)-5xy^4}$

$y'=\frac{y^5}{1-2y\tan^2(y^2)-5xy^4}$

$y'=\frac{y^5}{1+2y\sec^2(y^2)+5xy^4}$

$y'=\frac{5y^4}{1-2y\sec^2(y^2)-5xy^4}$

Correct answer:

$y'=\frac{y^5}{1-2y\sec^2(y^2)-5xy^4}$

Explanation:

To find the derivative with respect to y, we use implicit differentiation, which is an application of the chain rule

$y=\tan(y^2)+xy^5$

$y'=\sec^2(y^2)(2yy')+y^5+5xy^4(y')$

$y'-2yy'\sec^2(y^2)-5xy^4y'=y^5$

$y'(1-2y\sec^2(y^2)-5xy^4)=y^5$

$y'=\frac{y^5}{1-2y\sec^2(y^2)-5xy^4}$

Report an Error

Example Question #73 : Applications Of Derivatives

Given that y=y(x) , find the derivative of the function

$y=2xy^3+x\cos(y)$

Possible Answers:

$y'=\frac{2y^3+\cos(y)}{1-x\sin(y)-6xy^2}$

$y'=\frac{2y^3+\cos(y)}{1+x\sin(y)-6xy^2}$

$y'=\frac{2y^3+\cos(y)}{1+\sin(xy)-6xy^2}$

$y'=\frac{2y^3+\sin(y)}{1+x\sin(y)-6xy^2}$

Correct answer:

$y'=\frac{2y^3+\cos(y)}{1+x\sin(y)-6xy^2}$

Explanation:

To find the derivative with respect to y, we use implicit differentiation, which is an application of the chain rule

$y=2xy^3+x\cos(y)$

$y'=2y^3+6xy^2y'+\cos(y)-x\sin(y)y'$

$y'+xy'\sin(y)-6xy^2y'=2y^3+\cos(y)$

$y'(1+x\sin(y)-6xy^2)=2y^3+\cos(y)$

$y'=\frac{2y^3+\cos(y)}{1+x\sin(y)-6xy^2}$

Report an Error

Example Question #71 : Applications Of Derivatives

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

$xy+\ln(y)=x$

Possible Answers:

$\frac{-y}{xy+1}$

$\frac{y-y^2}{xy+y}$

$\frac{y-y^2}{xy+1}$

$\frac{y^2-y}{x}$

Correct answer:

$\frac{y-y^2}{xy+1}$

Explanation:

To find $\frac{\mathrm{d} y}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.
Taking $\frac{\mathrm{d} y}{\mathrm{d} x}$ of both sides of the equation, we get

$y+x\frac{\mathrm{d} y}{\mathrm{d} x}+\frac{1}{y}\frac{\mathrm{d} y}{\mathrm{d} x}=1$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$ , $\frac{\mathrm{d} }{\mathrm{d} x} \ln(x)=\frac{1}{x}$

Note that for every derivative of a function with y, the additional term $\frac{\mathrm{d} y}{\mathrm{d} x}$ appears; this is because of the chain rule, where y=g(x) , so to speak, for the function it appears in.

Using algebra to solve for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{\mathrm{d} y}{\mathrm{d} x}= \frac{1-y}{x+\frac{1}{y}}= \frac{y-y^2}{xy+1}$

Report an Error

Example Question #611 : Derivatives

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

$3y+x\tan(y)=2$

Possible Answers:

$\frac{-\tan(y)}{3-x\sec^2(y)}$

$\frac{\tan(y)}{3+x\sec^2(y)}$

$\frac{-\tan(y)}{3+x\sec^2(y)}$

$\frac{-\tan(y)}{3+\sec^2(y)}$

Correct answer:

$\frac{-\tan(y)}{3+x\sec^2(y)}$

Explanation:

To find $\frac{\mathrm{d} y}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.
Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$3 \frac{\mathrm{d} y}{\mathrm{d} x} +\tan(y)+x\sec^2(y)\frac{\mathrm{d} y}{\mathrm{d} x}=0$

The following derivative rules were used:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \tan(x)=\sec^2(x)$

Using algebra to solve for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{-\tan(y)}{3+x\sec^2(y)}$

Report an Error

Example Question #81 : Applications Of Derivatives

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

x^2+xy=4

Possible Answers:

-2x-y

$\frac{2x-y}{x}$

$\frac{1}{x}$

$\frac{-2x-y}{x}$

Correct answer:

$\frac{-2x-y}{x}$

Explanation:

$2x+y+x\frac{\mathrm{d} y}{\mathrm{d} x}=0$

using the following rules:

Using algebra to solve for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{-2x-y}{x}$ .

Report an Error

Example Question #1071 : Ap Calculus Ab

Use implicit differentiation to calculate the equation of the line tangent to the equation $2x^{2}+y^{2}=9$ at the point (2,1).

Possible Answers:

y=4x-9

y=4x+9

y=-4x-9

y=-4x+9

Correct answer:

y=-4x+9

Explanation:

Differentiate both sides of the equation: $\frac{\mathrm{d} }{\mathrm{d} x}(2x^{2}+y^{2}=9)$

Simplify: $4x+\frac{\mathrm{d} }{\mathrm{d} x}y^{2}=0$

Use implicit differentiation to differentiate the y term: $4x+2y\frac{dy}{dx}=0$

Subtract 4x from both sides of the equation: $2y\frac{dy}{dx}=-4x$

Divide both sides of the equation by 2y: $\frac{dy}{dx}=\frac{-4x}{2y}=\frac{-2x}{y}$

Plug in the appropriate values for x and y to find the slope of the tangent line: $m=\frac{-2(2)}{(1)}=-4$

Use slope-intercept form to solve for the equation of the tangent line: y=mx+b=y=-4x+b

Plug in the appropriate values of x and y into the equation, to find the equation of the tangent line: 1=(2)(-4)+b

Solve for b: 1=-8+b

b=9

Solution: y=-4x+9

Report an Error

Example Question #21 : Implicit Differentiation

Find $\frac{\mathrm{d} z}{\mathrm{d} x}$ , where is a function of x.

Possible Answers:

$\frac{3-z}{x+2z}$

$\frac{3-2z}{x}$

$\frac{-z}{x+2z}$

Correct answer:

$\frac{3-z}{x+2z}$

Explanation:

To find $\frac{\mathrm{d} z}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.
Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$z+x\frac{\mathrm{d} z}{\mathrm{d} x}+2z\frac{\mathrm{d} z}{\mathrm{d} x}=3$

and the derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$
Note that for every derivative of a function with z, the additional term $\frac{\mathrm{d} z}{\mathrm{d} x}$ appears; this is because of the chain rule, where z=g(x), so to speak, for the function it appears in.

Using algebra to solve, we get

$\frac{\mathrm{d} z}{\mathrm{d} x}=\frac{3-z}{x+2z}$

Report an Error

View AP Calculus AB Tutors

Blake
Certified Tutor

Vanderbilt University, Bachelors, Neuroscience.

View AP Calculus AB Tutors

Siddharth
Certified Tutor

University of Petroleum and Energy Studies and, Masters in Business Administration, Aviation Management.

View AP Calculus AB Tutors

Andrew
Certified Tutor

University of Wisconsin-Stevens Point, Bachelor of Science, Mathematics. University of Wisconsin-Oshkosh, Master of Science, ...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Philadelphia, ACT Tutors in Houston, Computer Science Tutors in Dallas Fort Worth, Physics Tutors in Atlanta, Algebra Tutors in New York City, ISEE Tutors in Dallas Fort Worth, Physics Tutors in Phoenix, Statistics Tutors in Atlanta, Math Tutors in Phoenix, Statistics Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Seattle, GRE Courses & Classes in Houston, SSAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Boston, ACT Courses & Classes in Miami, MCAT Courses & Classes in Houston, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Washington DC, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Phoenix, MCAT Test Prep in Chicago, ACT Test Prep in Miami, LSAT Test Prep in Washington DC, ISEE Test Prep in Miami, SAT Test Prep in Boston, SSAT Test Prep in Chicago, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in New York City, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Implicit differentiation

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #71 : Applications Of Derivatives

Example Question #601 : Derivatives

Example Question #71 : Applications Of Derivatives

Example Question #72 : Applications Of Derivatives

Example Question #73 : Applications Of Derivatives

Example Question #71 : Applications Of Derivatives

Example Question #611 : Derivatives

Example Question #81 : Applications Of Derivatives

Example Question #1071 : Ap Calculus Ab

Example Question #21 : Implicit Differentiation

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: