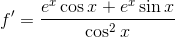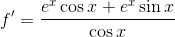Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivatives

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=\frac{e^x}{\cos{x}}$

Possible Answers:

$f'=\frac{e^x\cos{x}-e^x\sin{x}}{\cos^2{x}}$

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos{x}}$

$f'=\frac{e^x\cos{x}+e^x\cos{x}}{\cos^2{x}}$

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Correct answer:

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Explanation:

To find the derivative of a quotient, you apply the quotient rule:

$\frac{\mathrm{d} }{\mathrm{d} x}(\frac{f(x)}{g(x)})=\frac{{f'(x)g(x)-f(x)g'(x)}}{(g(x))^2}$

In our case, we have f(x)=e^x and $g(x)=\cos{x}$

Using the function from the problem statement and taking its derivative, we get

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Report an Error

Example Question #42 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=\frac{\cos{x}}{2x^2}$

Possible Answers:

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{2x^4}$

$f'=\frac{-2x^2\sin{x}-4x\sin{x}}{4x^4}$

$f'=\frac{-x^2\sin{x}-4x\cos{x}}{2x^4}$

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Correct answer:

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Explanation:

To find the derivative of a quotient, you apply the quotient rule:

$\frac{\mathrm{d} }{\mathrm{d} x}(\frac{f(x)}{g(x)})=\frac{{f'(x)g(x)-f(x)g'(x)}}{(g(x))^2}$

In our case, we have $f(x)=\cos{x}$ and g(x)=2x^2

Using the function from the problem statement and taking its derivative, we get

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Report an Error

Example Question #43 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=2x\sin{x}+2\cos{x}$

Possible Answers:

$f'=2x\cos{x}$

$f'=2x\cos{x}+2\sin{x}$

$f'=-2x\cos{x}$

$f'=2\cos{x}$

Correct answer:

$f'=2x\cos{x}$

Explanation:

To find the derivative of the function, you must apply the product rule. The product rule is as follows

$\frac{\mathrm{d} }{\mathrm{d} x}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)$

In the first part of the expression, we have f(x)=2x and $g(x)=\sin{x}$ , and in the second part of the expression we have f(x)=2 and $g(x)=\cos{x}$

Using the product rule from above, we have

$f'=2\sin{x}+2x\cos{x}-2\sin{x}=2x\cos{x}$

Report an Error

Example Question #44 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=5x^2\tan{x}$

Possible Answers:

$f'=10x\tan{x}+5x^2\sec^2{x}$

$f'=10\tan{x}+5x^2\sec^2{x}$

$f'=10x\tan{x}-5x^2\sec^2{x}$

$f'=10x\tan{x}+5x^2\sec{x}$

Correct answer:

$f'=10x\tan{x}+5x^2\sec^2{x}$

Explanation:

To find the derivative of the function, you must apply the product rule. The product rule is as follows

$\frac{\mathrm{d} }{\mathrm{d} x}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)$

In this case, we have f(x)=5x^2 and $g(x)=\tan{x}$

Using the product rule from above, we have

$f'=10x\tan{x}+5x^2\sec^2{x}$

Report an Error

Example Question #45 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative.

$\frac{2x+1}{x^2}$

Possible Answers:

$\frac{1}{x}$

x-1

2x+1

Correct answer:

x-1

Explanation:

Use the quotient rule to find the derivative.

$\frac{d}{dx}\frac{2x+1}{x^2}=\frac{x^2(2)-2x(2x+1)}{2x}$

$=\frac{2x^2-4x^2-2x}{2x}$

$=\frac{-2x^2-2x}{2x}$

$=\frac{-x^2-x}{x}=x-1$

Report an Error

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative.

$x^2\sin (x)$

Possible Answers:

$x\cos (x)+2x\cos (x)$

$x^2\cos (x)+2x\cos (x)$

$x\cos (x)+2x\sin (x)$

$x^2\cos (x)+2x\sin (x)$

Correct answer:

$x^2\cos (x)+2x\sin (x)$

Explanation:

Use the product rule to find the derivative.

$x^2\cos (x)+2x\sin (x)$

Report an Error

Example Question #47 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

f(x)=4x^3+10x

Possible Answers:

f'(x)=12x^3+10

f'(x)=x^4+2x^2

f'(x)=12x^2+10

f'(x)=12x^2+10x

Correct answer:

f'(x)=12x^2+10

Explanation:

To find the derivative of a sum, we take the derivative of each part of the sum independently. Additionally, we apply the rules of differentiation that tell us

$\frac{\mathrm{d} }{\mathrm{d} x}x^n=nx^{n-1}$

Differentiating the function from the problem statement, we get

$f'(x)=\frac{\mathrm{d} }{\mathrm{d} x}(4x^3)+\frac{\mathrm{d} }{\mathrm{d} x}(10x)$

f'(x)=12x^2+10

Report an Error

Example Question #48 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function using the product and quotient rules:

$f(x)=\frac{5x\tan(x)}{\cos(x)}$

Possible Answers:

$f'(x)=(\cos(x)\left (5\tan(x)+5x\sec^2(x))+5x\tan(x)\sin(x))/\cos^2(x)$

$f'(x)=(\cos(x)\left (5\tan(x)+5x\sec^2(x))+5x\tan(x)\sin(x))/\sin^2(x)$

$f'(x)=\cos(x)\left (5\tan(x)+5x\sec^2(x))+5x\tan(x)\sin(x)$

$f'(x)=(\cos(x)\left (10\tan(x)+5\sec^2(x))+5x\tan(x)\sin(x))/\cos^2(x)$

Correct answer:

$f'(x)=(\cos(x)\left (5\tan(x)+5x\sec^2(x))+5x\tan(x)\sin(x))/\cos^2(x)$

Explanation:

Using the product and quotient rules to solve the problem, we get

$f'(x)=\frac{\cos(x)*\frac{\mathrm{d} }{\mathrm{d} x}(5x\tan(x))-(5x\tan(x))*\frac{\mathrm{d} }{\mathrm{d} x}(\cos(x))}{\cos^2(x)}$

The product rule is used when taking $\frac{\mathrm{d} }{\mathrm{d} x}(5x\tan(x))=\frac{\mathrm{d} }{\mathrm{d} x}(5x)*\tan(x)+5x*\frac{\mathrm{d} }{\mathrm{d} x}\tan(x)$

The final answer is

$f'(x)=(\cos(x)\left (5\tan(x)+5x\sec^2(x))+5x\tan(x)\sin(x))/\cos^2(x)$

Report an Error

Example Question #49 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function using the product rule:

f(x)=(x^3+3)(2x-1)

Possible Answers:

f'(x)=8x+3x^2+5

f'(x)=11x^3+4

f'(x)=8x^3-3x^2+6

f'(x)=8x^2+3x^2+6

Correct answer:

f'(x)=8x^3-3x^2+6

Explanation:

Using the product rule, we ge f'(x)=8x^3-3x^2+6 t

$f'(x)=(2x-1)*\frac{\mathrm{d} }{\mathrm{d} x}(x^3+3)+(x^3+3)*\frac{\mathrm{d} }{\mathrm{d} x}(2x-1)$

Simplifying,

f'(x)=3x^2(2x-1)+2(x^3+3)

f'(x)=6x^3-3x^2+2x^3+6

f'(x)=8x^3-3x^2+6

Report an Error

Example Question #51 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of y=5x^3e^x

Possible Answers:

15x^2e^x+5x^3

15x^2e^x

15x^2e^x+5x^3xe

5x^2e^x(3+x)

none of these answers

Correct answer:

5x^2e^x(3+x)

Explanation:

So whenever you have two distinct functions that are multiplied by each other, you will be using the product rule. So when looking at a function, see if you can separate it into two. In this case, we can see there is the function:

5x^3 and the function e^x .

So lets call those f(x) and g(x)

Then the product rule is that the derivative of f(x)g(x ) is:

f'(x)g(x)+f(x)g'(x) .

Then calculate to find:

f'(x)=15x^2 and g'(x)=e^x to give an answer of:

f'(x)g(x)+f(x)g'(x)=15x^2e^x+5x^3e^x

which simplifies to:

5x^2e^x(3+x)

Report an Error

View AP Calculus AB Tutors

Shrikar
Certified Tutor

University of South Florida-Main Campus, Bachelor of Science, Biomedical Sciences.

View AP Calculus AB Tutors

Vandana
Certified Tutor

Jawaharlal Nehru Technological University, Bachelor of Technology, Civil Engineering. Florida International University, Maste...

View AP Calculus AB Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Boston, ISEE Tutors in San Diego, Algebra Tutors in Los Angeles, English Tutors in Houston, Statistics Tutors in Denver, Physics Tutors in Houston, SAT Tutors in Washington DC, Physics Tutors in Denver, Algebra Tutors in Washington DC, Chemistry Tutors in Dallas Fort Worth

Popular Courses & Classes

SAT Courses & Classes in Seattle, MCAT Courses & Classes in Seattle, Spanish Courses & Classes in Chicago, MCAT Courses & Classes in Chicago, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Seattle, GMAT Courses & Classes in Miami

Popular Test Prep

LSAT Test Prep in Seattle, LSAT Test Prep in Philadelphia, MCAT Test Prep in Houston, GRE Test Prep in Atlanta, SSAT Test Prep in New York City, LSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Washington DC, SAT Test Prep in Miami, SAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivatives

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #42 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #43 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #44 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #45 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #47 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #48 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #49 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #51 : Derivative Rules For Sums, Products, And Quotients Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: