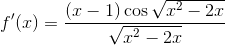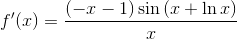All AP Calculus AB Resources
Example Questions
Example Question #151 : Computation Of The Derivative
Given the function 
Given the function 
where 




Example Question #152 : Computation Of The Derivative
Given the function 
Given the function 
where 




Example Question #453 : Ap Calculus Ab
Given the function 
Given the function 
where 




Example Question #153 : Computation Of The Derivative
Given the function 
Given the function 
where 




Example Question #462 : Ap Calculus Ab
Find 
Let 
Then
can be rewritten as
Let
The function can now be rewritten as
Applying the chain rule twice:
Example Question #241 : Derivatives
Find the derivative of the function
To find the derivative of the function, you must apply the chain rule, which is as follows:
Using the function from the problem statement, we have that

Following the rule, we get
Example Question #242 : Derivatives
Find the derivative of the function
To find the derivative of the function, you must apply the chain rule, which is as follows:
Using the function from the problem statement, we have that

Following the rule, we get
Example Question #243 : Derivatives
Find 
None of the other choices gives the correct response.
Let
Then
and
Apply the chain rule:
Substitute back for 
Apply the sum rule:
After some simple algebra:
Example Question #244 : Derivatives



The expressions with 


Find the indefinite integral of both sides:
Set 


Substitute back:

Raise 

The correct choice is
Example Question #245 : Derivatives
Find the derivative using the chain rule.
Use the chain rule to find the derivative:
Thus,
Certified Tutor
All AP Calculus AB Resources





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971070/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971096/gif.latex)
![\small \small \small \small z'(x)=[-\sin (5-x^{10})][-10x^9]=10x^{9}\sin(5-x^{10})](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971102/gif.latex)




![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971087/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971061/gif.latex)