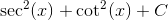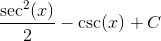Rewrite the integrand as follows:

.

The integral can be rewritten as

Now, use -substitution, setting . It follows that 

The limits of integration can be rewritten as

The integral becomes

Integrate:

,

the correct response.

The integral can be solved by using a variable substitution

, 

Replacing  with , we get our final answer, which is

We solve the problem by making a variable substitution

, 

The integral then becomes

Substituting  for , we get our final answer

To integrate, it is easiest to break the integral into the sum of two integrals:

To integrate the first integral, we must make the following substitution:

The derivative was found using the rule itself.

Rewriting the first integral in terms of u and integrating, we get

which was found using the rule itself.

Replacing u with our original x term, we get

The second integral is equal to

and was found using the following rule:

Adding our two results, and combining the two constants of integration into a single integration constant, we get

The simplest path to follow when trying to integrate a lot of trig expressions is often to put everything in terms of sin(x) and cos(x). Doing this for the above expressions yields:

Next, we look for expressions that we know how to integrate, based on the following facts:

And, of course, the simpler derivatives of sin(x) and cos(x).

Looking for these above expressions in our integral, we note that 

Breaking this up into two integrals, we see that the second immediately can be simplified into -csc(x) + C. The first, while a bit more tricky, just requires you to realize that sec(x)tan(x) is the derivative of sec(x). Thus, if you use a substitution of variables (u-sub) with u = sec(x), you will get,

and

In this form, it is clear to see that the integral is just   where u = sec(x)

Combining our two integrals, we get a final answer of 

To evaluate the integral, we make a variable substitution for 

, 

The integral then becomes

Substituting  back in for , the final answer is

So, unlike with derivatives, there is no equivalent for the chain rule of the product rule for integrals. Anytime you see a function within a function (a compound function) and/or the product of more than one function inside an integral, you can't just take the integral. In this case, we are able to perform a substitution. So the goal with a substitution is to replace all of the x variables (including dx) with another variable (we use u, and du).

So we can set 

which gives us 

So this changes our integral to:

Which just turns out to:

 the C is added because we have no bounds for the integral.

After replacing u for what is originally was, we end up with:

So, unlike with derivatives, there is no equivalent for the chain rule of the product rule for integrals. Anytime you see a function within a function (a compound function) and/or the product of more than one function inside an integral, you can't just take the integral. In this case, we are able to perform a substitution. So the goal with a substitution is to replace all of the x variables (including dx) with another variable (we use u, and du).

 For this problem, we set 

This gives us 

So the thing to note with substitutions is that the  that you choose has to have a derivative that is also in the integral. If the  had not been in the integral, then this substitution would not work. 

So making these substitutions gives:

solving this integral gives: 

Substituting the u back into the equation gives us a final answer of:

We are going to use U-substitution

Looking at the original

Let 

Then

And now we can use our anti derivative rules (don't forget your constant!)

Finally, substitute back in for u

To evaluate the integral, we must make the following substitution:

Rewriting the integral in terms of u and solving, we get

The integral was found using the following rule:

To finish, rewrite the answer in terms of x: