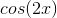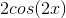Use the addition and subtraction properties of integrals to break the integral into 3 separate integrals:Evaluate the second integral: 

Re-write the third integral as follows: 

Evaluate the third integral:

Make the following substitution to evaluate the first integral:     

Apply the substitution to the first integral: 

Evaluate the integral: 

Substitute the value for u back into the equation: 

Combine the answers of the three integrals into one equation:  

Solution: 

Make the following substitution:     

Apply the substitution to the integrand: 

Evaluate the integral: 

Re-substitute the value of u: 

Solution: 

There are a lot of pieces inside this integral. There are trigonometry functions, exponential functions, and a rational arrangement. Lots of possibilities.

This is where u-substitution is best. Try making u represent various parts and see if du gets all the other parts. After doing this enough times, you will see that we should make u be the exponent of the e.

Let's write the inner fraction as an x with a negative exponent

Now we differentiate and see what we get for du. This will require the chain rule. The outer structure is the , which requires trig functions integration rules, and the chained inner structure is a power rule arrangement

Recall these derivatives:

Applying these we get

Simplifying gives us

This perfectly matches all remaining parts of our integral. Lets rewrite everything using u and du

This matches the basic integral form,

Thus, when we integrate we get

Rewriting back in terms of x, we get

This is our answer.

There are two ways to evaluate this integral:

(1) Rewrite in terms of sine and cosine and evaluate

(2) Break up the into and

In this explanation, we will do option (2)

Breaking up the , we get the following integral

Notice that the part is the derivative of . Lets use this fact and make the following u-substitution

Differentiating to find du, we use the chain rule and power rule:

This du accounts for all the other parts of the integral. Rewriting in terms of u, we get

This follows the basic integral form, .

Applying this rule, we get

Now we "un-substitute" back to x terms, using our original substitution, .

This gives us

This is the correct answer.

This integral can be evaluated using u-substitution. There aren't any groups raised to an exponent so we won't try the power rule for integration. Instead we notice that the integral is still a giant fraction. We will try to match this basic integral form:

Let's make the denominator our .

Differentiate to get .

This may not look like the numerator, but if we factor out an x, it will.

Now we have all the pieces matched perfectly. Let's make to substitution.

Applying the basic integral form from before, we get

Putting everything back in terms of x, we get

.

This is the correct answer.

The question is asking when the derivative is negative and the second derivative is positive. First, taking the derivative, we get

Solving for the zero's, we see  hits zero at  and . Constructing an interval test,

, we want to know the sign's in each of these intervals. Thus, we pick a value in each of the intervals and plug it into the derivative to see if it's negative or positive. We've chosen -5, 0, and 1 to be our three values.

Thus, we can see that the derivative is only negative on the interval .

Repeating the process for the second derivative,

The reader can verify that this equation hits 0 at -4/3. Thus, the intervals to test for the second derivative are 

.  Plugging in -2 and 0, we can see that the first interval is negative and the second is positive.

Because we want the interval where the second derivative is positive and the first derivative is negative, we need to take the intersection or overlap of the two intervals we got:

If this step is confusing, try drawing it out on a number line -- the first interval is from -3 to 1/3, the second from -4/3 to infinity. They only overlap on the smaller interval of -4/3 to 1/3.

Thus, our final answer is 

If  is decreasing, then its derivative is negative. The derivative of  is , so this is telling us that  is negative.

For  to be decreasing,  would have to be negative, which we don't know.

 being negative has nothing to do with its slope. 

For  to be decreasing, its derivative  would need to be negative, or, alternatively  would have to be concave down, which we don't know.

Thus, the only correct answer is that  is negative.

We see the answer is  when we use the product rule.

To understand why the answer is

 ,

you must understand that the derivative of    

is actually

 .

Next, you must understand that the derivative of 

is actually

.

 can be treated as a composition of the functions 

 and .

 in terms of  and  is actually , which means 

 since  in  is substituted with .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the component composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

is 

Step 1: Only look at the outermost function f(x) first, then differentiate it

Step 2: Look at the next function g(x), keep it inside the other function f'(x). 

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

So,  substitute f'(x), g(x) and g'(x) for the expressions you found before:

And now you have found the correct answer. 

-------------------------------------------------------------------------------------------

To sum it up, you multiply the derivative of the outermost functions by the derivative if the inner function while keeping the next inner functions the the same in every step until you are out of functions to find the derivative of. This also applies to more complicated functions. For instance,

If we have 

then it's derivative would be

Notice how the factors become less complicated as you differentiate it or as you look from left to right.  

If you are unsure of the pattern, look at the pattern in these equations

To understand why the answer is

 ,

you must understand that the derivative of    

is actually

 .

Next, you must understand that the derivative of 

is actually

.

 can be treated as a composition of the functions 

 and .

 in terms of  and  is actually , which means 

 since  in  is substituted with .

This means in order to differentiate the equation, you must use the chain rule. The chain rule tells us that in order to differentiate a composition function, you must differentiate all of the composite functions in the reverse order that they are applied to the variable, one step at a time and multiply the results together.

the derivative of

is 

Step 1: Only look at the outermost function f(x) first, then differentiate it

Step 2: Look at the next function g(x), keep it inside the other function f'(x). 

Step 3: Differentiate the the next function g(x) but multiply it by f'(g(x))

So,  substitute f'(x), g(x) and g'(x) for the expressions you found before:

And now you have found the correct answer. 

-------------------------------------------------------------------------------------------

To sum it up, you multiply the derivative of the outermost functions by the derivative if the inner function while keeping the next inner functions the the same in every step until you are out of functions to find the derivative of. This also applies to more complicated functions. For instance,

If we have 

then it's derivative would be

Notice how the factors become less complicated as you differentiate it or as you look from left to right.  

If you are unsure of the pattern, look at the pattern in these equations