All AP Calculus AB Resources
Example Questions
Example Question #22 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #23 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #24 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Example Question #25 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Let 
A relative maximum of the graph of 
The graph of 
At a relative minimum 



First, find 
Differentiate the individual terms using the Constant Multiple and Power Rules:
Set this equal to 0:
Either:





Now take the second derivative, again using the sum rule:
Differentiate the individual terms using the Constant Multiple and Power Rules:
Substitute 

Therefore, 

Now. substitute 

Therefore, 

Example Question #26 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Estimate the integral of 
Because our 
Example Question #27 : Riemann Sums (Left, Right, And Midpoint Evaluation Points)
Use Left Riemann sums with 4 subintervals to approximate the area between the x-axis, 


To use left Riemann sums, we need to use the following formula:

where 



,
and 

This fancy equation approximates using boxes. We can rewrite this fancy equation by writing 




Think of 

This is basically 
Now we need to determine what 

To find 


In short,
Now we need to find the x values that are the left endpoints of each of the 4 subintervals. Left endpoints because we are doing Left Riemann sums.
The left most x value happens to be the smaller of the overall endpoints given in the question. In other words, since we only care about the area from 



Now we know that 
To find the next endpoint, 

Add the 
And repeat to find
Now that we have all the pieces, we can plug them in.
plug each value into 
This is the final answer, which is an approximation of the area under the function.
Example Question #1 : Points Of Inflection
Find the points of inflection of
There are no points of inflection.
We will find the points of inflection by setting our second derivative to zero.
Take the derivative again,
then set this equal to zero and reverse foil,
These are our points of inflection.
Example Question #2 : Points Of Inflection
If 




To find the inflection points of 








On the unit circle, the values 




To prove that 




Hence 



Example Question #1 : Points Of Inflection
At what value(s) does the following function have an inflection point?
No inflection points.



Inflection points of a function occur when the second derivative equals zero. Therefore, we simply need to take two derivatives of our function, and solve.
Therefore, the two values that makes this function go to zero are
Example Question #4 : Points Of Inflection
Determine the points of inflection for the following function:
This function has no points of inflection
To determine the points of inflection, we must find the value at which the second derivative of the function changes in sign.
First, we find the second derivative:
The derivatives were found using the following rules:

Next, we find the values at which the second derivative of the function is equal to zero:
Using the critical value, we now create intervals over which to evaluate the sign of the second derivative:
Notice how at the bounds of the intervals, the second derivative is neither positive nor negative.
Evaluating the sign simply by plugging in any value on the given interval into the second derivative function, we find that on the first interval, the second derivative is negative, while on the second interval, the second derivative is positive. The second derivative changed sign 
Certified Tutor
Certified Tutor
All AP Calculus AB Resources




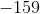

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-2)=-17\\&f(1)=-4\\&f(4)=-16\\&f(7)=-16\\&\text{Although the total interval has a length of }9\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }3\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-2}^{7}f(x)\approx3[(-17)+(-4)+(-16)]\\&\int_{-2}^{7}f(x)\approx-111\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945098/gif.latex)





![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(5)=-3\\&f(11)=8\\&f(17)=11\\&f(23)=-3\\&\text{Although the total interval has a length of }18\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }6\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{5}^{23}f(x)\approx6[(-3)+(8)+(11)]\\&\int_{5}^{23}f(x)\approx96\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945125/gif.latex)





![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\\&\text{It is essentially a sum of n rectangles, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\\&\text{In our case, we have function values over an interval:}\\&f(-8)=-10\\&f(1)=12\\&f(10)=-1\\&f(19)=11\\&\text{Although the total interval has a length of }27\\&\text{Notice the points are equidistant, with }3\text{ intervals between.}\\&\text{Each equidistant interval has length: }9\\&\text{Since we are using the left point of each interval, we disregard the larst function value:}\\&\int_{-8}^{19}f(x)\approx9[(-10)+(12)+(-1)]\\&\int_{-8}^{19}f(x)\approx9\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/945129/gif.latex)


![x= \sqrt[4]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971492/gif.latex)
![x=- \sqrt[4]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971493/gif.latex)














































+[(-1)^4+1](1)+ [(0)^4+1](1)+[(1)^4+1](1)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1061094/gif.latex)
![[16 + 1]+ [1 + 1]+ [0+ 1]+ [1 + 1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1061095/gif.latex)








































