All AP Calculus AB Resources
Example Questions
Example Question #110 : Derivative At A Point
Example Question #511 : Derivatives
Example Question #512 : Derivatives
Example Question #513 : Derivatives
Example Question #514 : Derivatives
Example Question #515 : Derivatives
Example Question #516 : Derivatives
Example Question #41 : Approximate Rate Of Change From Graphs And Tables Of Values
Example Question #1 : How To Graph Functions Of Points Of Inflection
Which of the following functions has exactly one point of inflection?

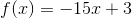




For any function, a point of inflection occurs when 



A linear equation does not have any points of inflection, nor does a quadratic equation or exponential function.
A function with an order higher than three has multiple points of inflection.
Example Question #871 : Ap Calculus Ab
Over what interval is the graph of 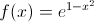
The concavity of a function is determined by its second derivative. Whenever the second derivative of a function is positive, the function is said to be concave upward.
We will find the first derivative of 
Next, we will differentiate the first derivative of 
We must now determine where 
We can divide both sides of the equation by 

This is only true when 



Certified Tutor
All AP Calculus AB Resources



















































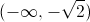


![f'(x)=\frac{d}{dx}[e^{1-x^2}]=e^{1-x^2}\cdot \frac{d}{dx}[1-x^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24804/gif.latex)

![f''(x)=\frac{d}{dx}[-2xe^{1-x^2}]=e^{1-x^2}\cdot \frac{d}{dx}[-2x] + -2x\cdot \frac{d}{dx}[e^{1-x^2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/24806/gif.latex)








