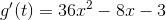Maximum's and minimums of functions can take place where the derivative is 0 or undefined. To find out where this occurs, we take the derivative.

As you can see, the derivative will be 0 at .

At this point, we have three options:

We can plug them all into the original equation and see which are the biggest and which are the smallest.

We can use the first derivative interval test to see which are mins and which are maxes.

We can use the second derivative test to see which are mins and which are maxes.

As we're likely going to have to plug them all into the equation anyway, and the problem doesn't ask to classify the points as local mins or maxes, the first approach is the most time effective. Plugging in our points we find that  ;  ;

Before we determine the answer, it's important to remember that the global maxes and mins on a closed domain can occur at the endpoints, and on an open domain, may not exist. For this problem, we're given a quartic that faces upwards. Thus, there is no global maximum because the graph shoots off to infinity on either side. On the other hand, there is a global min because the graph is continuous and does not go down to negative infinity.

As we know the min must occur at one of the points we've determined above, we can see that we have a global min of -123 at x = 4 and no global maximum.

Also note, as a bit of terminology, that a global maximum or minimum value is a value that occurs at a point. Thus our answer isn't that the maximum value is (4, -123), but just -123.

This question is an optimization problem. This question asks to find the distance to run along the beach that minimizes the time it takes to get to the swimmer in the water. To minimize time, we need to construct an equation, where time is a function of one variable. Fortunately, the equation

can be solved for time, and this is how we will create the equation we need.

Solving this equation for time gives

We have two Rates. Running on the beach, and Swimming in the water. So we have two times to consider:

and

Adding these two times gives the total time to get to the person in the water.

We are given the rates that the life guard can run and swim, 10ft/sec and 4ft/sec respectively. The variable is how far to swim down the beach.

Labeling the distance the life guard runs as will make the math somewhat difficult, where as labeling the distance the life guard runs as will make the math a little nicer. We just need to remember that we did this. The picture below shows the labeling used in this explanation.

With this labeling, the distance the life guard runs is , and the distance the life guard swims is by Pythagorean Theorem.

Plugging the distances and rates into our Time equation gives:

This expresses Time as a function of one variable, . This is what we need to minimize. To do this we will find the relative minimum of this function. So we find the first derivative. First, we will do a little algebra and split the into two fractions and rewrite the square root as an exponent to make the derivative easier to compute.

Now we find the derivative. The derivative of is .

The derivative of  is .

We use the chain rule for . Doing so gives

Assembling the pieces results in the following derivative

To find the critical points, we substitute 0 in for Time'.

To solve for , we move the  to the opposite side and then cross multiply.

 Now we can divide by 4 on both sides to isolate the square root, then reduce the resulting 10/4 to 5/2. Then we square both sides to eliminate the square root.

We know need to move the terms to the same side, the right side in this explanation Remember that we will need to get the common denominator to combine them.

Multiply both sides by to isolate . Then square root both sides. We will not need to incorporate the when we square root, since  is a physical distance.

Since the question asks us to approximate the answer to the nearest hundredth, we can plug into a calculator to get a decimal. Doing so gives approximately x=43.64 ft.

However, this is not our final answer. Recall that we defined the distance the life guard ran as . So we need to subtract x=43.64 from 200 to find what the question is asking for. 

Doing this we get our final answer to be .

Since the rectangle has one corner on the origin, (0,0), and the opposite corner at a point (x,y) on the graph, we can set the width = x, and the length = y. 

The area of a rectangle is , so for this problem, .

Since we are trying to maximize the area, we need to express area as a function of only one variable. Right now we have two variables. The way to fix this is to subsitute one variable, like , with an equivalent function of .

Most problems give a relationship between the two variables. In this problem, the equation of the quarter-ellipse, , is the relationship we need.

We can substitute the in the Area equation with what is equals.

Now we have the equation of what we want to maximize, Area , written in terms of only one variable, x. Now we can find the relative maximum by finding the derivative.

Before finding the derivative, it will be helpful to rewrite the square root as an exponent.

We will need to use the product rule, , and use chain rule for . Doing this, we get:

Now we find the critical points of the derivative by setting it equal to zero and solving. We will simplify the derivative slightly at the same time. We can multiply the fractions in the second part, an move the  down to the denominator to remove the negative from the exponent. This gives us:

Now we can solve for x. First, subtract the term to the left side.

Now multiply both sides by denominator, , in order to eliminate the fraction.

The is multiplied by the same group, so we add their exponents, 1/2 + 1/2, which is 1. So we don't need to write the new exponent, since 1 is understood.

Since the power on the group is 1, we can distribute the -6 through it.

Moving all the terms to the left, and the -6 to the right, we get:

Divide both sides by 2 to isolate

Now square root both sides.

Since the graphs domain is given as , we can ignore the negative answer and use the positive answer.

Now we know the width is . To find the length, we need to find . 

Plug into the graph's equation to find .

We need to get the square root out of the denominator. To do this we mulitply the numerator and denominator by .

Thus, the length of the rectangle should be .

Now we know the dimensions of the rectangle, that maximize its area:

width=

length =

First we must find out critical points by setting  equal to zero.

Then we reverse foil to get

These are our critical points.  We now must test values on each interval defined by our critical points in order to determine the sign of  on each interval. 

Our intervals to check are

We have many choices, but let's choose 

Thus on our first interval  is positive meaning  is increasing.

On our second interval  is negative meaning  is decreasing.

And on our third interval  is positive meaning  is increasing.

What does the sign of the first derivative tell us about whether a function is increasing or decreasing?

The first derivative test is used to tell whether a function is increasing or decreasing at a certain point or interval. 

To use this test, first find the derivative of your function. Then, plug in the values for the point(s) and see what sign you get on your values. 

If the value of your first derivative is negative, then your function is decreasing. If the value of your first derivative is positive, your original function is increasing. If your first derivative is 0, then you have a point of inflection in your original function.

Use the first derivative test to tell whether f(c) is increasing or decreasing when c=24

Begin by finding the first derivative of f(c)

Next, plug in 24 for c and find the sign of our first derivative.

Now, our first derivative is positive, so our original function must be increasing.

Find the derivative of g(t) and tell whether g(t) is increasing or decreasing on the interval [5,6]

First, find the derivative by decreasing each exponent by 1 and multiplying the coefficient by that number.

Next, plug in our two endpoints of our interval to see what the sign of g'(t) is.

Now, clearly these are both negative, and every point between them will be negative. This means that function g(t) is decreasing on this interval.

Tell whether f is increasing or decreasing when . How do you know?

To test for increasing/decreasing, we need to find the first derivative.

In this case, we can use the power rule to do all our differentiation.

Power rule:

We will use this on each term in order to find our first and then second derivative.

For each term, we will decrease the exponent by 1, and then multiply by the original exponent.

Now, we need to find the sign of f'(-12). This will tell us if it is increasing or decreasing.

So, we get

So, 

f(x) is decreasing, because 

To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.

The first derivative of the function is equal to

and was found using the following rule:

Next, we must find the critical values, at which the first derivative is equal to zero:

Using the critical values, we now create intervals over which to evaluate the sign of the first derivative:

Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.

On the first interval, the first derivative is negative, while on the remaining intervals, the first derivative is positive. Thus, the function is decreasing on the first interval, . 

To determine the intervals on which the function is decreasing, we must determine the intervals on which the function's first derivative is negative.

The first derivative of the function is equal to

and was found using the following rule:

Next, we must find the critical values, at which the first derivative is equal to zero:

The square root of a negative number is not valid for a critical value, so we only have one critical value for this function.

Using the critical value, we now create intervals over which to evaluate the sign of the first derivative:

Notice how at the bounds of the intervals, the first derivative is neither positive nor negative.

On the first interval, the first derivative is positive, and on the second interval, the first derivative is positive as well. The function is therefore never decreasing because the first derivative is never negative.