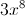.  However,  cannot be simplified any further because the terms have different exponents.

(Like terms are terms that have the same variables with the same exponents. Only like terms can be combined together.)

Apply the laws of exponents as follows:

1. Factor 

***notice that the two fractions now share a factor in the denominator***

2. Create a common denominator between the two terms

3. Simplify

To add any fractions together, they must first have a common denominator. We can obtain a common denominator of  if we multiply the first fraction by  and the second one by . We therefore obtain:

From there, we need to take out the radical in the denominator by multiplying by , as follows:

From here, we can simplify the radicals above by finding their prime factors:

and

.

We are therefore left with , which can be separated and reduced to our final answer,

In this form, the exponents are multiplied: .

In multiplication problems, the exponents are added.

In division problems, the exponents are subtracted.

It is important to know the difference.

 times  gives us , while  times 4 gives us . So it equals .

Be sure to distribute the  along with its coefficient.

With this problem, you need to take the trinomials out of parentheses and combine like terms. Since the two trinomials are being added together, you can remove the parentheses without needing to change any signs:

The next step is to combine like terms, based on the variables. You have two terms with , two terms with , and two terms with no variable. Make sure to pay attention to plus and minus signs with each term when combining like terms:

With this problem, you need to distribute the two fractions across each of the trinomials. To do this, you multiply each term inside the parentheses by the fraction outside of it:

The next step is to combine like terms, based on the variables. You have two terms with , two terms with , and two terms with no variable. Make sure to pay attention to plus and minus signs with each term when combining like terms. Since you have a positive and negative , those two terms will cancel out:

When multiplying these two trinomials, you'll need to use a modified form of FOIL, by which every term in the first trinomial gets multiplied by every term in the second trinomial. One way to do this is to use the grid method.

You can also solve it piece by piece the way it is set up. First, multiply each of the three terms in the first trinomail by . Second, multiply each of those three terms again, this time by . Finally multiply the three terms again by .

Finally, you can combine like terms after this multiplication to get your final simplified answer: