All Algebra II Resources
Example Questions
Example Question #71 : Solving Absolute Value Equations
Solve.






Solve.
Step 1: Isolate the absolute value by subtracting 
Step 2: Divide -1 from both sides of the equation in order to get rid of the negative sign in front of the absolute value.
Step 3: Because this is an inequality, this equation can be solved in two parts as shown below.
Note: 


Step 4: Solve both parts.
Distribute the 
Subtract 
Divide both sides of the equation by 
Distribute the 
Subtract 
Divide both sides of the equation by 
Step 5: Combine both parts using "or".

Solution: 
Example Question #72 : Solving Absolute Value Equations
Solve for




Given: 
When given an absolute value recognize there are often multiple solutions. The reason why is best exhibited in a simpler example:
Given 




In the case of the more complicated equation 

To simplify the absolute value we must look at each of these cases:

Just like a normal equation with one unknown we will simplify it by isolating 

Next 

To check this solution it must be substituted in the original absolute value for 

so this becomes:
and the absolute value of 



Distribute the negative sign, which is just 
Next 
dividing by 
Checking this solution is done just as you did for the previous solution obtained.
Given 
substitute 
multiply 
so you obtain
adding
and the absolute value of 


Example Question #73 : Solving Absolute Value Equations
Solve for 





Solve for 

When given an absolute value equation recognize there are often multiple solutions. The reason why is best exhibited in a simpler example:
Given 




In the case of the more complicated equation 



When added together this gives 
thereby giving you
For the same reason as shown in the case of 

To simplify the absolute value we must look at each of these cases:
Let's start with the positive case:
Just like a normal equation with one unknown we will simplify it by isolating 

We can first subtract 


Next we can subtract 
Dividing both sides by 



so
To check this solution it must be substituted in the original absolute value for 

Simplify the equation by multiplying 


This leaves our equation with

Next add 
In order to simplify 

This leaves:
Similarly a common denominator is found for 



this leaves:
simplifying further gives you


Next let's solve for the negative case:
Distribute the negative sign, which is just 

Combine like terms:
This can be simplified to 

Checking this solution is done just as you did for the previous solution obtained.
Given
substitute 
Multiplying 

Multiplying 
So the equation simplifies to:
Next 

Now common denominators must be found for 
The common denominator for 




The common denominator of 

so
The simplified equation becomes
Through dividing 





so 
Example Question #71 : Absolute Value
Solve for 
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.

and
This gives us:

However, this question has an 




Our final solution is then
Example Question #71 : Solving Absolute Value Equations
Which values of 
Example Question #1 : Graphing Absolute Value Functions
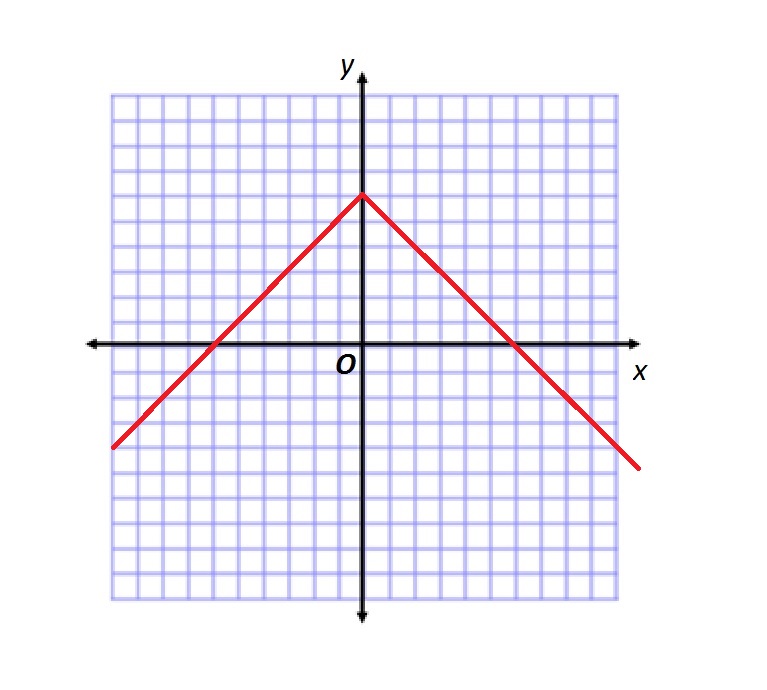
Refer to the above figure.
Which of the following functions is graphed?
Below is the graph of 

The given graph is the graph of 



The function graphed is therefore
Example Question #71 : Absolute Value

Refer to the above figure.
Which of the following functions is graphed?
Below is the graph of 

The given graph is the graph of 




The function graphed is therefore
Example Question #3 : Graphing Absolute Value Functions

Refer to the above figure.
Which of the following functions is graphed?
The correct answer is not given among the other responses.
Below is the graph of 

The given graph is the graph of 


The function graphed is therefore


Example Question #1 : Graphing Absolute Value Functions

What is the equation of the above function?
The formula of an absolute value function is 





Example Question #5 : Graphing Absolute Value Functions
Give the vertex of the graph of the function 
None of the other choices gives the correct response.
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 

The graph of this function can be formed by shifting the graph of 



Certified Tutor
All Algebra II Resources










































































































































