All Algebra II Resources
Example Questions
Example Question #71 : Solving And Graphing Logarithms
Solve 
The first thing we can do is combine all the log terms on the right side of the equation:
Next, we can take the coefficient from the left term and make it an exponent:
Now we can cancel the logs from both sides:
When we put 

Example Question #72 : Solving Logarithms
Solve 
First, we take the coefficient, 
Now we can cancel the logs:
When we check our answers, however, we notice that 
Example Question #72 : Solving And Graphing Logarithms
Solve 
First, we combine the log terms on the left of the equation:
Now we can cancel the logs on each side:
We can subtract 

Notice that 
Example Question #74 : Solving Logarithms
Solve 
The first thing we can do is move both log functions to one side of the equation:
Then we can combine the log functions (remember, when you add logs, we multiply the terms inside):
Now we can rewrite the equation in exponent form (and FOIL the multiplied terms):
We can collect all the terms on one side of the equation, and then solve the quadratic:
However, if we plug 
Example Question #75 : Solving Logarithms
Solve 
We first put both logs on one side of the equation:
Now we combine the log terms (remember, when we subtract logs we divide the terms inside):
We can now rewrite the equation in exponential form:
Anything raised to the 

Example Question #76 : Solving Logarithms
Solve 
We start by rewriting the equation in exponential form:
Now we can simplify:
Example Question #71 : Solving Logarithms
Solve 
We can either do this the long and proper way, or the simple and easy way.
The long way:
First, we move both logs to the same side of the equation:
Now we can combine the logs (reminder, when you subtract logs, you divide the terms inside of them):
Let's rewrite the equation in exponential form:
Anything raised to the 

The short way:
First, we cancel the log terms (because the base is the same, and all we have are the log terms):
Then we divide by 
Example Question #221 : Logarithms



so in this case it is

and
Example Question #1 : Graphing Logarithmic Functions
Give the 
to two decimal places.
The graph has no 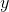
Set 
The 

Example Question #2 : Graphing Logarithmic Functions
Give the 
to two decimal places.
The graph has no 
Set 
The 

Certified Tutor
All Algebra II Resources






































































































