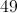Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #63 : Foil

Solve: 2(3-x)(5x+1)

Possible Answers:

-5x^3+14x+3

-10^2-32x+6

-10^2+32x+6

-10^2-28x+6

-10^2+28x+6

Correct answer:

-10^2+28x+6

Explanation:

Solve the binomials by using the FOIL method.

(3-x)(5x+1) = (3)(5x)+(3)(1)+(-x)(5x)+(-x)(1)

Simplify by distribution.

15x+3-5x^2-x

Combine like-terms.

-5x^2+14x+3

Rewrite the expression.

2(3-x)(5x+1)=2[-5x^2+14x+3] = -10^2+28x+6

The answer is: -10^2+28x+6

Report an Error

Example Question #251 : Intermediate Single Variable Algebra

Solve: (9-x)(2-4x)

Possible Answers:

4x^2-54x+18

4x^2-38x+18

-4x^2-38x+18

-4x^2-22x+18

-4x^2+22x+18

Correct answer:

4x^2-38x+18

Explanation:

Use the FOIL method to simplify this expression.

(w+x)(y+z) =wy+wz+xy+xz

Follow suit using the order given for (9-x)(2-4x) .

(9)(2)+(9)(-4x)+(-x)(2)+(-x)(-4x)

Simplify the terms.

18-36x-2x+4x^2

Combine like terms and rearrange the terms from highest to lowest order.

The answer is: 4x^2-38x+18

Report an Error

Example Question #90 : Understanding Quadratic Equations

Use the FOIL method to expand and simplify the expression:

(4x+4)(x-3)

Possible Answers:

4x^2+8x-12

4x^2-16x-12

4x^2-8x-12

4x^2+16x-12

4x^2-8x+12

Correct answer:

4x^2-8x-12

Explanation:

Remember, FOIL stands for First terms, Outer terms, Inner terms, Last terms, and goes as follows:

First Terms:

$({\color{Red} 4x}+4)({\color{Red} x}-3)={\color{Red} 4x^2}$

Outer Terms:

$({\color{Red} 4x}+4)(x{\color{Red} -3})=4x^2{\color{Red} -12x}$

Inner Terms:

$(4x{\color{Red} +4})({\color{Red} x}-3)=4x^2-12x{\color{Red} +4x}$

Last Terms:

$(4x{\color{Red} +4})(x{\color{Red} -3})=4x^2-12x+4x{\color{Red} -12}$

Combine like terms to give answer:

4x^2-8x-12

Report an Error

Example Question #1 : Understanding The Discriminant

Given $2x^{2}+3x-5=0$ , what is the value of the discriminant?

Possible Answers:

Correct answer:

Explanation:

In general, the discriminant is $b^{2}-4ac$ .

In this particual case $a=2, b=3\; and\; c=-5$ .

Plug in these three values and simplify: $(3)^{2}-4(2)(-5)= 49$

Report an Error

Example Question #1 : Discriminants

The equation

$4x ^{2} + Bx + 27= 0$

has two imaginary solutions.

For what positive integer values of is this possible?

Possible Answers:

$\left \{ 1, 2, 3,...11\right \}$

$\left \{ 1, 2, 3,...20\right \}$

$\left \{ 21, 22, 23, ... \right \}$

All positive integers

$\left \{ 12, 13, 14,...\right \}$

Correct answer:

$\left \{ 1, 2, 3,...20\right \}$

Explanation:

For the equation

$ax^{2} + bx + c = 0$

to have two imaginary solutions, its discriminant $b^{2} - 4ac$ must be negative. Set a = 4, c = 27 , b = B and solve for in the inequality

$b^{2} - 4ac < 0$

$B^{2} - 4 (4)(27)< 0$

$B^{2} - 432< 0$

$B^{2} < 432$

$\left | B \right | < \sqrt{432} \approx 20.8$

Therefore, if is a positive integer, it must be in the set $\left \{ 1, 2, 3,...20\right \}$ .

Report an Error

Example Question #3 : Discriminants

The equation

$3x ^{2} + Bx + 28= 0$

has two real solutions.

For what positive integer values of is this possible?

Possible Answers:

$\left \{ 1,2, 3,...,18 \right \}$

All positive integers

$\left \{ 1,2, 3,4\right \}$

$\left \{ 19, 20, 21, ...\right \}$

$\left \{ 5, 6, 7, ...\right \}$

Correct answer:

$\left \{ 19, 20, 21, ...\right \}$

Explanation:

For the equation

$ax^{2} + bx + c = 0$

to have two real solutions, its discriminant $b^{2} - 4ac$ must be positive. Set a = 3, c = 28, b = B and solve for in the inequality

$b^{2} - 4ac > 0$

$B^{2} - 4 (3)(28)> 0$

$B^{2} - 336> 0$

$B^{2} > 336$

$\left | B\right | > \sqrt{336} \approx 18.3$

Therefore, if is a positive integer, it must be in the set $\left \{ 19, 20, 21, ...\right \}$

Report an Error

Example Question #3 : Discriminants

What is the discriminant of the following quadratic equation? Are its roots real?

4x^2-9x+22

Possible Answers:

The equation's discriminant is and its roots are not real.

The equation's discriminant is and its roots are real.

The equation's roots are not real; therefore, it does not have a discriminant.

The equation's discriminant is and the its roots are not real.

The equation's discriminant is and its roots are real.

Correct answer:

The equation's discriminant is and the its roots are not real.

Explanation:

The "discriminant" is the name given to the expression that appears under the square root (radical) sign in the quadratic formula, b^2-4ac where , , and are the numbers in the general form of a quadratic trinomial: ax^2+bx+c . If the discriminant is positive, the equation has real roots, and if it is negative, we have imaginary roots. In this case, a=4 , b=-9 , and c=22 , so the discriminant is , and because it is negative, this equation's roots are not real.

Report an Error

Example Question #2 : Discriminants

Find the discriminant, $\Delta$ , in the following quadratic expression:

3x^2+5x-2

Possible Answers:

Correct answer:

Explanation:

Remember the quadratic formula:

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ .

The discriminant in the quadratic formula is the term that appears under the square root symbol. It tells us about the nature of the roots.

So, to find the discriminant, all we need to do is compute b^2-4ac for our equation, where a=3, b=5, c=-2 .

We get 25 - (-24) = 49 .

Report an Error

Example Question #1 : Discriminants

Choose the answer that is the most correct out of the following options.

How many solutions does the function f(x)=x^2-7x+2 have?

Possible Answers:

2 real solutions

1 real solution; 1 imaginary solution

2 imaginary solutions

No solution

1 real solution

Correct answer:

2 real solutions

Explanation:

The number of roots can be found by looking at the discriminant. The discriminant is determined by b^2-4ac . For this function, a=1 , b=-7 , and c=2 . Therfore, -7^2-(4)(1)(2)=41 . When the discriminant is positive, there are two real solutions to the function.

Report an Error

Example Question #6 : Discriminants

Determine the discriminant of the following quadratic equation f(x)=-x^2+4x+9 .

Possible Answers:

$\small 52$

$\small -20$

Correct answer:

$\small 52$

Explanation:

The discriminant is found using the equation b^2-4ac . So for the function -x^2+4x+9 , a=-1 , b=4 , and c=9 . Therefore the equation becomes 4^2-(4)(-1)(9)=52 .

Report an Error

View Algebra 2 Tutors

Pushpendra
Certified Tutor

university of allahabad, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Jordyn
Certified Tutor

University of Illinois at Chicago, Bachelor of Science, Biological and Physical Sciences.

View Algebra 2 Tutors

Dean
Certified Tutor

Florida Atlantic University, Master of Science, Mathematics.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in San Francisco-Bay Area, Math Tutors in Seattle, GMAT Tutors in Atlanta, French Tutors in Houston, Biology Tutors in Dallas Fort Worth, Spanish Tutors in Denver, ACT Tutors in Denver, ISEE Tutors in Boston, GRE Tutors in Washington DC, Statistics Tutors in Washington DC

Popular Courses & Classes

SSAT Courses & Classes in Chicago, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in New York City, SAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Phoenix, ACT Courses & Classes in Atlanta, ACT Courses & Classes in New York City, SAT Courses & Classes in Chicago

Popular Test Prep

ISEE Test Prep in Atlanta, ACT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, ACT Test Prep in Denver, ISEE Test Prep in New York City, ACT Test Prep in Atlanta, LSAT Test Prep in San Diego, SSAT Test Prep in Los Angeles, GMAT Test Prep in Seattle, ISEE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #63 : Foil

Example Question #251 : Intermediate Single Variable Algebra

Example Question #90 : Understanding Quadratic Equations

Example Question #1 : Understanding The Discriminant

Example Question #1 : Discriminants

Example Question #3 : Discriminants

Example Question #3 : Discriminants

Example Question #2 : Discriminants

Example Question #1 : Discriminants

Example Question #6 : Discriminants

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: