Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Functions and Graphs

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #71 : Inverse Functions

Define a function $f(x) = \frac{x-2}{2x}$ .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f^{-1}(x) = \frac{2}{2-x}$

$f^{-1}(x) = \frac{2}{1-2x}$

$f^{-1}(x) = \frac{2}{2+x}$

$f^{-1}(x) = \frac{2}{2x-1}$

$f^{-1}(x) = \frac{2}{2x+1}$

Correct answer:

$f^{-1}(x) = \frac{2}{1-2x}$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x) = \frac{x-2}{2x}$

$y= \frac{x-2}{2x}$

Switch the positions of and :

$x= \frac{y-2}{2y}$

Solve for - that is, isolate it on one side - as follows:

Split the expression at right into the difference of two separate expressions:

$x = \frac{y}{2y} - \frac{2}{2y}$

Simplify:

$x = \frac{1}{2} - \frac{1}{y}$

Add $\frac{1}{y} - x$ to both sides:

$x + \frac{1}{y} - x = \frac{1}{2} - \frac{1}{y} + \frac{1}{y} - x$

$\frac{1}{y} = \frac{1}{2} - x$

Simplify the expression at right:

$\frac{1}{y} = \frac{1}{2} - \frac{2x}{2}$

$\frac{1}{y} = \frac{1-2x}{2}$

Take the reciprocal of both sides:

$y= \frac{2}{1-2x}$

Replace with $f^{-1}(x)$ :

$f^{-1}(x) = \frac{2}{1-2x}$

Report an Error

Example Question #272 : Introduction To Functions

Define a function $f(x) = \sqrt[3]{4x-9}$ .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f^{-1}(x) =\frac{1}{4} x^{3} + \frac{729}{4}$

$f^{-1}(x) =\frac{1}{4} x^{3} + \frac{27}{4}x^{2}+\frac{243}{4}x+ \frac{729}{4}$

$f^{-1}(x) =\frac{1}{4} x^{3} + \frac{9}{4}$

$f^{-1}(x) =\frac{1}{4} x^{3} - \frac{27}{4}x^{2}+\frac{243}{4}x- \frac{729}{4}$

$f^{-1}(x) =\frac{1}{4} x^{3} + 9$

Correct answer:

$f^{-1}(x) =\frac{1}{4} x^{3} + \frac{9}{4}$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x) = \sqrt[3]{4x-9}$

$y = \sqrt[3]{4x-9}$

Switch the positions of and :

$x = \sqrt[3]{4y-9}$

$\sqrt[3]{4y-9} = x$

Solve for - that is, isolate it on one side - as follows:

Raise both sides to the third power:

$\left (\sqrt[3]{4y-9} \right )^{3}= x^{3}$

$4y-9 = x^{3}$

Add 9 to both sides:

$4y-9 + 9 = x^{3} + 9$

$4y = x^{3} + 9$

Multiply both sides by $\frac{1}{4}$ , distributing on the right side:

$\frac{1}{4} \cdot 4y =\frac{1}{4} \cdot ( x^{3} + 9)$

$y =\frac{1}{4} \cdot x^{3} + \frac{1}{4} \cdot 9$

$y =\frac{1}{4} x^{3} + \frac{9}{4}$

Replace with $f^{-1}(x)$ :

$f^{-1}(x) =\frac{1}{4} x^{3} + \frac{9}{4}$

Report an Error

Example Question #71 : Inverse Functions

Define a function $f(x)= \frac{x}{x-1}$ .

True or false: f(x) is its own inverse.

Possible Answers:

False

True

Correct answer:

True

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x)= \frac{x}{x-1}$

$y = \frac{x}{x-1}$

Switch and :

$x = \frac{y}{y-1}$

Solve for - that is, isolate on one side of the equation - as follows:

Multiply both sides by y -1 , distributing on the right side:

$x\cdot (y-1) = \frac{y}{y-1} \cdot (y-1)$

$x\cdot y-x\cdot 1 = y$

x y-x = y

Add x-y to both sides to get all terms to the left, then factor out :

x y-x+ x- y = y + x- y

x y - y =x

$x \cdot y -1 \cdot y =x$

(x -1 ) y =x

Divide both sides by x-1 :

$\frac{(x -1 ) y}{x -1 } =\frac{x}{x -1 }$

$y =\frac{x}{x -1 }$

Replace with $f^{-1}(x)$ :

$f^{-1}(x) =\frac{x}{x -1 }$

Therefore, $f^{-1}(x)= f(x)$ , and f(x) is indeed its own inverse.

Report an Error

Example Question #274 : Introduction To Functions

Define a function $f(x) = 3 e ^{x} + 4$ .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f^{-1}(x)=\ln \left (\frac{1}{3} x - \frac{4}{3} \right )$

$f^{-1}(x)=\ln \left (\frac{1}{3} x -4 \right )$

$f^{-1}(x)=\log \left (\frac{1}{3} x - \frac{4}{3} \right )$

$f^{-1}(x)=\log \left (\frac{1}{3} x -4 \right )$

None of the other choices gives the correct response.

Correct answer:

$f^{-1}(x)=\ln \left (\frac{1}{3} x - \frac{4}{3} \right )$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x) = 3 e ^{x} + 4$

$y= 3 e ^{x} + 4$

Switch the positions of and :

$x= 3 e ^{y} + 4$

$3 e ^{y} + 4 = x$

Solve for - that is, isolate it on one side.

First, subtract 4:

$3 e ^{y} + 4 - 4 = x - 4$

$3 e ^{y} = x - 4$

Multiply by $\frac{1}{3}$ and distribute on the right:

$\frac{1}{3} \cdot 3 e ^{y} =\frac{1}{3} \cdot (x - 4)$

$e ^{y} =\frac{1}{3} \cdot x - \frac{1}{3} \cdot 4$

$e ^{y} =\frac{1}{3} x - \frac{4}{3}$

Take the natural logarithm of both sides:

$\ln e ^{y} =\ln \left (\frac{1}{3} x - \frac{4}{3} \right )$

$y =\ln \left (\frac{1}{3} x - \frac{4}{3} \right )$

Replace with $f^{-1}(x)$ :

$f^{-1}(x)=\ln \left (\frac{1}{3} x - \frac{4}{3} \right )$

Report an Error

Example Question #271 : Introduction To Functions

Relation

Which is true of the relation graphed above?

Possible Answers:

The relation is not a function.

The relation is a function, and it has an inverse.

The relation is a function, but it does not have an inverse.

Correct answer:

The relation is not a function.

Explanation:

A relation is a function if and only if it passes the Vertical Line Test (VLT) - that is, no vertical line exists that passes through its graph more than once. From the diagram below, we see that at least one such line exists:

Relation

The relation fails the VLT, so it is not a function.

Report an Error

Example Question #792 : Algebra Ii

Untitled

The above table shows a function with domain $\left \{ -3, -2, -1, 0, 1, 2, 3 \right \}$ .

True or false: f(x) has an inverse function.

Possible Answers:

True

False

Correct answer:

True

Explanation:

A function f(x) has an inverse function if and only if, for all a,b in the domain of f(x) , if $a \ne b$ , it follows that $f(a) \ne f(b)$ . In other words, no two values in the domain can be matched with the same range value.

If we order the rows by range value, we see this to be the case:

Untitled

If follows that f(x) has an inverse function.

Report an Error

Example Question #801 : Algebra Ii

Define a function $f(x) = \frac{5}{x- 7}$ .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f(x) = \frac{7x+5}{5}$

$f^{-1}(x) =\frac{7x+ 5 }{x}$

$f(x) = \frac{5x+ 7}{5}$

$f^{-1}(x) =\frac{7x- 5 }{x}$

$f(x) = \frac{x- 7}{5}$

Correct answer:

$f^{-1}(x) =\frac{7x+ 5 }{x}$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x) = \frac{5}{x- 7}$

$y = \frac{5}{x- 7}$

Switch the positions of and :

$x = \frac{5}{y- 7}$ ,

or,

$\frac{5}{y- 7} = x$

Solve for - that is, isolate it on one side.

Take the reciprocals of both sides:

$\frac{y- 7} {5}= \frac{1}{x}$

Multiply both sides by 5:

$5 \cdot \frac{y- 7} {5}=5 \cdot \frac{1}{x}$

$y- 7 =\frac{5}{x}$

Add 7:

$y- 7 + 7 =\frac{5}{x} + 7$

$y =\frac{5}{x} + 7$

The right expression can be simplified as follows:

$y =\frac{5}{x} + \frac{7x}{x}$

$y =\frac{7x+ 5 }{x}$

Replace with $f^{-1}(x)$ :

$f^{-1}(x) =\frac{7x+ 5 }{x}$

Report an Error

Example Question #271 : Introduction To Functions

Define a function $f(x) = e^{x-3}$ .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f^{-1}(x)= \ln x^{3}$

$f^{-1}(x)= \ln \frac{x}{3}$

$f^{-1}(x)= \ln \frac{x}{e^{3}}$

$f^{-1}(x)= \ln 3x$

$f^{-1}(x)= \ln x e^{3}$

Correct answer:

$f^{-1}(x)= \ln x e^{3}$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

$f(x) = e^{x-3}$

$y= e^{x-3}$

Switch the positions of and :

$x= e^{y-3}$ ,

$e^{y-3} = x$

Take the natural logarithm of both sides:

$\ln e^{y-3} = \ln x$

By definition, $\ln e^{a}= a$ , so

$y-3 = \ln x$

Add 3 to both sides:

$y-3 +3 = \ln x + 3$

$y = 3 + \ln x$

Replace with $f^{-1}(x)$ :

$f^{-1}(x)= 3 + \ln x$

This is not given among the choices; however, remember that by one of the properties of logarithms,

$a = \ln e^{a}$ ,

$f^{-1}(x)= \ln e^{3} + \ln x$

By another property, $\ln M + \ln N = \ln MN$ , so

$f^{-1}(x)= \ln (e^{3} \cdot x)$

$f^{-1}(x)= \ln x e^{3}$ ,

which is among the choices and is the correct answer.

Report an Error

Example Question #81 : Inverse Functions

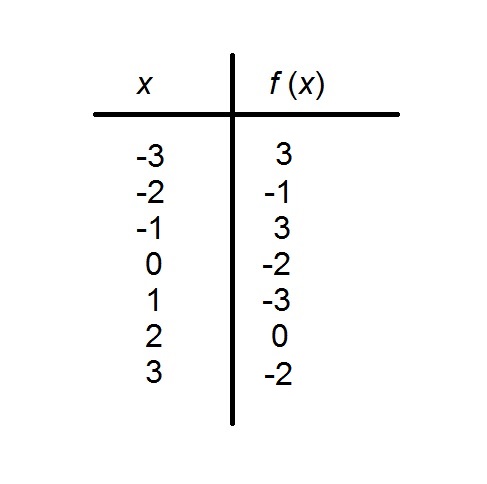
Untitled

The above table shows a function with domain $\left \{ -3, -2, -1, 0, 1, 2, 3 \right \}$ .

True or false: f(x) has an inverse function.

Possible Answers:

True

False

Correct answer:

False

Explanation:

If we order the rows by range value, we see this to not be the case:

Untitled

f(0)= f(3) = -2 and f(-1) = f(-3) = 3 . Since two range values exist to which more than one domain value is matched, the function has no inverse.

Report an Error

Example Question #82 : Inverse Functions

Define a function f(x) = 7x + 15 .

Which statement correctly gives $f^{-1}(x)$ ?

Possible Answers:

$f^{-1}(x)= \frac{1}{7}x+ \frac{15}{7}$

$f^{-1}(x)= \frac{1}{7}x- 15$

None of these

$f^{-1}(x)= \frac{1}{7}x+ 15$

$f^{-1}(x)= \frac{1}{7}x- \frac{15}{7}$

Correct answer:

$f^{-1}(x)= \frac{1}{7}x- \frac{15}{7}$

Explanation:

The inverse function $f^{-1}(x)$ of a function f(x) can be found as follows:

Replace f(x) with :

f(x) = 7x + 15

y= 7x + 15

Switch the positions of and :

x= 7y + 15 , or

7y+ 15 = x

Solve for - that is, isolate it on one side.

First, subtract 15:

7y+ 15- 15 = x - 15

7y = x - 15

Multiply by $\frac{1}{7}$ :

$\frac{1}{7} \cdot 7y =\frac{1}{7} \cdot \left ( x - 15 \right )$

Distribute:

$y =\frac{1}{7} \cdot x -\frac{1}{7} \cdot 15$

$y= \frac{1}{7}x- \frac{15}{7}$

Replace with $f^{-1}(x)$ :

$f^{-1}(x)= \frac{1}{7}x- \frac{15}{7}$ ,

the correct response.

Report an Error

View Algebra 2 Tutors

Pushpendra
Certified Tutor

university of allahabad, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Jordyn
Certified Tutor

University of Illinois at Chicago, Bachelor of Science, Biological and Physical Sciences.

View Algebra 2 Tutors

Dean
Certified Tutor

Florida Atlantic University, Master of Science, Mathematics.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Philadelphia, GMAT Tutors in Washington DC, GRE Tutors in New York City, GRE Tutors in Atlanta, GMAT Tutors in Boston, SSAT Tutors in Los Angeles, ISEE Tutors in San Diego, Chemistry Tutors in Dallas Fort Worth, MCAT Tutors in Philadelphia, Physics Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Seattle, GRE Courses & Classes in Houston, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Chicago, MCAT Courses & Classes in New York City, SSAT Courses & Classes in Los Angeles, ACT Courses & Classes in San Diego, LSAT Courses & Classes in Atlanta, ACT Courses & Classes in Philadelphia, LSAT Courses & Classes in Denver

Popular Test Prep

GRE Test Prep in Seattle, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Atlanta, SSAT Test Prep in Seattle, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in San Diego, MCAT Test Prep in Chicago, MCAT Test Prep in Houston, ISEE Test Prep in Miami, ACT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Functions and Graphs

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #71 : Inverse Functions

Example Question #272 : Introduction To Functions

Example Question #71 : Inverse Functions

Example Question #274 : Introduction To Functions

Example Question #271 : Introduction To Functions

Example Question #792 : Algebra Ii

Example Question #801 : Algebra Ii

Example Question #271 : Introduction To Functions

Example Question #81 : Inverse Functions

Example Question #82 : Inverse Functions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: