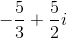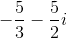Algebra II : Complex Imaginary Numbers
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #1 : Complex Imaginary Numbers
Example Question #1 : Irrational Numbers
Multiply:
Use the FOIL technique:
Example Question #1 : Complex Imaginary Numbers
Evaluate
You cannot divide by complex numbers
To divide by a complex number, we must transform the expression by multiplying it by the complex conjugate of the denominator over itself. In the problem, 
We can then combine like terms and rewrite all 
Our final answer is therefore
Example Question #2 : Imaginary Numbers
Simplify the following product:
Multiply these complex numbers out in the typical way:
and recall that 
which is our final answer.
Example Question #2 : Complex Imaginary Numbers
Identify the real part of
none of the above.
A complex number in its standard form is of the form: 
The real part in this problem is 1.
Example Question #1961 : Mathematical Relationships And Basic Graphs
Simplify:
To add complex numbers, find the sum of the real terms, then find the sum of the imaginary terms.
Example Question #1 : Imaginary Numbers
Simplify:
To add complex numbers, find the sum of the real terms, then find the sum of the imaginary terms.
Example Question #2 : Imaginary Numbers
Simplify:
To add complex numbers, find the sum of the real terms, then find the sum of the imaginary terms.
Example Question #3 : Imaginary Numbers
Simplify:
To subtract complex numbers, subtract the real terms together, then subtract the imaginary terms.
Example Question #3 : Complex Imaginary Numbers
Simplify:
To subtract complex numbers, subtract the real terms, then subtract the imaginary terms.
All Algebra II Resources
