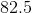Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Graphing Data

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #433 : Basic Statistics

If varies indirectly with $\sqrt{x}$ and when x=4 , y=12.3 due to the effect of a constant, what is the value of when x=17 ?

Possible Answers:

y=5.97

y=25.36

y=50.71

y=16.49

y=0.24

Correct answer:

y=5.97

Explanation:

Since varies indirectly with $\sqrt{x}$ , $y=\frac{K}{\sqrt{x}}$

1. Solve for when y=12.3 and x=4 .

$y=\frac{K}{\sqrt{x}}$

$12.3=\frac{K}{\sqrt{4}}$

$12.3= \frac{K}{2}$

K=24.6

2. Use the equation you found to solve for when x=17 .

$y=\frac{24.6}{\sqrt{x}}$

$y=\frac{24.6}{\sqrt{17}}=5.97$

Report an Error

Example Question #2 : Variable Relationships

varies directly with $x^{2}$ . If x=5, y=75 , what is if x=10 ?

Possible Answers:

250

150

300

100

Correct answer:

300

Explanation:

1. Since varies directly with $x^{2}$ :

$y=Kx^{2}$ with K being some constant.

2. Solve for K using the x and y values given:

$75=K(5^{2})$

75=K(25)

K=3

3. Use the equation you solved for to find the value of y:

$y=3x^{2}$

$y=3(10^{2})$

y=300

Report an Error

Example Question #4 : Identifying Variable Relationships

varies inversely with $x^{3}$ . If x=2, y=2 , then what is equal to when x=5 ?

Possible Answers:

0.654

0.128

0.226

0.197

Correct answer:

0.128

Explanation:

1. Since varies indirectly with $x^{3}$ :

$y=\frac{K}{x^{3}}$

2. Use the given x and y values to determine the value of K:

$2=\frac{K}{2^{3}}$

$2=\frac{K}{8}$

K=16

3. Using the equation along with the value of K, find the value of y when x=5:

$y=\frac{16}{x^{3}}$

$y=\frac{16}{5^{3}}$

y=0.128

Report an Error

Example Question #5 : Identifying Variable Relationships

varies directly with $\sqrt[3]{x}$ and when x=8, y=3 . What is when x=27 ?

Possible Answers:

4.5

5.5

Correct answer:

4.5

Explanation:

1. Since varies directly with $\sqrt[3]{x}$ :

$y=K\sqrt[3]{x}$

2. Use the values given for x and y to solve for K:

$y=K\sqrt[3]{x}$

$3=K\sqrt[3]{8}$

3=K(2)

$K=\frac{3}{2}$

3. Use your new equation with the K you solved for to solve for y when x=27:

$y=(\frac{3}{2})\sqrt[3]{27}$

$y=(\frac{3}{2})(3)=4.5$

Report an Error

Example Question #441 : Basic Statistics

varies inversely with $\sqrt{x}$ . When $x=4,\ y=0.5$ . What is the value of when x=100 ?

Possible Answers:

$\frac{1}{8}$

$\frac{1}{4}$

$\frac{1}{20}$

$\frac{1}{10}$

Correct answer:

$\frac{1}{10}$

Explanation:

1. Since y varies indirectly with $\sqrt{x}$ :

$y=\frac{K}{\sqrt{x}}$

2. Solve for K using the x and y values given:

$0.5=\frac{K}{\sqrt{4}}$

$0.5=\frac{K}{2}$

K=1

3. Using the equation you created by solving for K, find y when x=100:

$y=\frac{1}{\sqrt{x}}$

$y=\frac{1}{\sqrt{100}}$

$y=\frac{1}{10}$

Report an Error

Example Question #1 : Interpolations

Given the two following points, use interpolation to determine the best estimate for the value f(24.75)

(24,81) , (25,93)

Possible Answers:

82.5

91.5

Correct answer:

Explanation:

Using our two known points, we can use interpolation to determine the value at any point between them with the following formula:

$\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}$

Where (x_1,y_1) is our first given point, (x_2,y_2) is our second given point, and (x,y) is the point we want to find. We know our two given points, as well as the x value of our unknown point, so now all we must do is plug in all of our known values and solve for y, our only unknown:

$\frac{93-81}{25-24}=\frac{y-81}{24.75-24}$

$12=\frac{y-81}{0.75}$

$y-81=9\rightarrow y=f(24.75)=90$

Report an Error

Example Question #1 : Interpolations

The output of a factory in units per day versus the number of employees working is plotted on the graph below, with the following data points collected:

(Workers, Units of output per day):

$\left(100,1300\right)$

$\left(75,1050\right)$

$\left(200,2300\right)$

$\left(225,2550\right)$

Assuming a linear relationship, interpolate to find how many units will be made per day if 110 workers are present.

Linear_interp

Possible Answers:

$1400\textup{ units}$

$1375\textup{ units}$

$1370\textup{ units}$

$1335\textup{ units}$

$1380\textup{ units}$

Correct answer:

$1400\textup{ units}$

Explanation:

We want to do a linear interpolation since the relationship between workers and units can be assumed to be linear. This means there is a constant slope between the points, so the slope between two known points will be equal to the slope between the point we are trying to find and some known point. This is expressed in the relation:

$\frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0}$ ,

where and are the points we want to find and (x_1,y_1) and (x_0,y_0) are known. We choose the known points to be those that are just to the left and right of the point we are trying to find,

(100,1300) and (200,2300) .

Plugging these into our interpolation formula and knowing x=110 , we can find , the units output per day.

$\frac{y-1300}{110-100}=\frac{2300-1300}{200-100}$ .

Simplifying and rearranging to solve for :

y=1400 .

So there are 1400 units produced when the number of workers is 110 .

Report an Error

Example Question #1 : Interpolations

Given the points $\left ( 30,51\right )$ and $\left ( 20,36\right )$ , use linear interpolation to find the value of when x=26.5 .

Possible Answers:

44.60

42.38

45.75

49.99

Correct answer:

45.75

Explanation:

Use the formula for interpolation to determine the value of y:

$\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{x-x_{1}}$

We will use (30, 51) as our x2 and y2 and (20, 36) as our x1 and y1 and we will solve for y using 26.5 for x.

$\frac{51-36}{30-20}=\frac{y-36}{26.5-20}$

$\frac{15}{10}=\frac{y-36}{6.5}$

$\frac{3}{2}(6.5)=y-36$

y=45.75

Report an Error

Example Question #1 : Interpolations

Given $\left ( 15,10\right )$ and $\left ( 30,15\right )$ use linear interpolation to find when x=17.9 .

Possible Answers:

10.54

10.97

11.34

11.21

Correct answer:

10.97

Explanation:

Use the formula for interpolation:

$\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{x-x_{1}}$

We will use (30, 15) as x2 and y2, (15, 10) as x1 and y1, and solve for y when x=17.9:

$\frac{15-10}{30-15}=\frac{y-10}{17.9-15}$

$\frac{5}{15}=\frac{y-10}{2.9}$

$(\frac{5}{15})(2.9)=y-10$

y=10.97

Report an Error

Example Question #5 : Interpolations

Mary measures her height every year on her birthday, starting at 11 until she turns 16. She wants to make a table with all the information gathered, but discovers she lost the piece of paper on which she wrote her height down on her 14^th birthday. Her incomplete table looks like this:

Age (years)	Height (inches)
11	47.5
12	50.25
13	53
14	?
15	58.5
16	61.25

Using the method of linear interpolation, which of the following is the closest estimate of Mary's height on her 14^th birthday?

Possible Answers:

$55.75\:in$

$57\ in$

$53.\bar{3}\:in$

$56\:in$

Not enough information given in the problem.

Correct answer:

$55.75\:in$

Explanation:

Using linear interpolation means that we draw a line between the points on our data set and use that line to estimate a value that lies between two data points; in this case, we have the data from Mary's 13^thand 15^th birthdays, so we can describe a line between those two points and estimate her height at 14. Our line will be written in slope-intercept form:

y=mx+b

Where the variable represents Mary's Age in years and the variable represents her height in inches. First, we need to find the slope. Using 2 points on our table (13,53) and (15,58.5) as point 1 and point 2, respectively, we plug these values into our slope formula:

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{(58.5-53)}{(15-13)}=\frac{5.5}{2}=2.75$

Next, we find the y-intercept by plugging in our slope (which we just found) and a point from our table (we'll stick with (13,53) ) and solving for :

53=(2.75)(13)+b

Simplify:

53=35.75+b

Subtract 35.75 from both sides to solve for :

b=17.25

The equation of our interpolation line is:

y=(2.75)x+17.25

So, to get an estimate of Mary's height on her 14^th birthday, we plug in x=14 and solve for :

y=(2.75)(14)+17.25=38.5+17.25=55.75

Our estimate of Mary's height at x=14 is $55.75\:in$

Report an Error

View Algebra 2 Tutors

Ana Maria
Certified Tutor

Florida International University, Bachelor of Science, Mathematics Teacher Education.

View Algebra 2 Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View Algebra 2 Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Los Angeles, ACT Tutors in Boston, Reading Tutors in Chicago, SAT Tutors in New York City, Biology Tutors in Atlanta, Calculus Tutors in Houston, SAT Tutors in Philadelphia, SSAT Tutors in Atlanta, GMAT Tutors in Philadelphia, English Tutors in Los Angeles

Popular Courses & Classes

SSAT Courses & Classes in New York City, GMAT Courses & Classes in New York City, ISEE Courses & Classes in Phoenix, GRE Courses & Classes in Denver, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in New York City, LSAT Courses & Classes in New York City, ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Dallas Fort Worth, SAT Test Prep in Seattle, LSAT Test Prep in Phoenix, MCAT Test Prep in Washington DC, MCAT Test Prep in Seattle, ACT Test Prep in New York City, GRE Test Prep in New York City, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Dallas Fort Worth, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Graphing Data

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #433 : Basic Statistics

Example Question #2 : Variable Relationships

Example Question #4 : Identifying Variable Relationships

Example Question #5 : Identifying Variable Relationships

Example Question #441 : Basic Statistics

Example Question #1 : Interpolations

Example Question #1 : Interpolations

Example Question #1 : Interpolations

Example Question #1 : Interpolations

Example Question #5 : Interpolations

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: