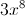Algebra II : Basic Single-Variable Algebra
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #81 : Variables
Simplify the expression:
The fraction cannot be simplified further.
When dividing polynomials, subtract the exponent of the variable in the numberator by the exponent of the same variable in the denominator.
If the power is negative, move the variable to the denominator instead.
First move the negative power in the numerator to the denominator:
Then subtract the powers of the like variables:
Example Question #111 : Basic Single Variable Algebra
Simplify:
(Like terms are terms that have the same variables with the same exponents. Only like terms can be combined together.)
Example Question #21 : Simplifying Expressions
Simplify:
Apply the laws of exponents as follows:
Example Question #112 : Basic Single Variable Algebra
Simplify the expression:
1. Factor
***notice that the two fractions now share a factor in the denominator***
2. Create a common denominator between the two terms
3. Simplify
Example Question #22 : Simplifying Expressions
Add and simplify the following rational expression:
No real solution
To add any fractions together, they must first have a common denominator. We can obtain a common denominator of 
From there, we need to take out the radical in the denominator by multiplying by 
From here, we can simplify the radicals above by finding their prime factors:
and
We are therefore left with 
Example Question #113 : Basic Single Variable Algebra
Simply:
In this form, the exponents are multiplied: 
In multiplication problems, the exponents are added.
In division problems, the exponents are subtracted.
It is important to know the difference.
Example Question #4662 : Algebra 1
Find the product:
Example Question #1954 : Algebra Ii
Distribute:
Be sure to distribute the 
Example Question #31 : Polynomials
Evaluate the following:
With this problem, you need to take the trinomials out of parentheses and combine like terms. Since the two trinomials are being added together, you can remove the parentheses without needing to change any signs:
The next step is to combine like terms, based on the variables. You have two terms with 
Example Question #1 : How To Add Trinomials
Evaluate the following:
With this problem, you need to distribute the two fractions across each of the trinomials. To do this, you multiply each term inside the parentheses by the fraction outside of it:
The next step is to combine like terms, based on the variables. You have two terms with 
All Algebra II Resources
