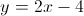To find the equation of a line, we need to know the slope and a point that passes through the line.  We can then use the equation  where m is the slope of the line, and  a point on the line.  For parallel lines, the slopes are the same.  The slope of  is 3, so the slope of the parallel line will be 3 as well.  We know that the parallel line needs to contain the point (0,1), so we have all of the information we need.  We can now use the equation 

The equation of a line is written in the following format: 

1) The first step, then, is to find the slope, .

 is equal to the change in  divided by the change in .

So,

2) Next step is to find . We can find values for  and  from any one of the given points, plug them in, and solve for .

Let's use (4,3)

So, 

Then we just fill in our value for , and we have  as a function of .

When an equation is in the  form, its slope is  and its y-intercept is . Thus, we need an equation with an  of 4 and a  of 6, which would be 

Use the point-slope formula to find the equation:

Start by using point-slope form:

Multiply the right side by the distributive property:

Then, convert to standard form:

Slope-intercept form is , where  is the slope and  is the y-intercept.  To rewrite the original equation in slope-intercept form, you must isolate the  variable: 

Now, divide each side by 20 so that  stands alone and simplify, and you are left with the slope-intercept form of the equation:

Let .

First, calculate the slope between the two points.

Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for .

Using slope-intercept form, where we know and , we can see that the equation for this line is .

To find the equation of this line, we need to know its slope and y-intercept. Let's find the slope first using our general slope formula.

The points are  and .  In this case, our points are (–3,0) and (2,5). Therefore, we can calculate the slope as the following:

Our slope is 1, so plug that into the equation of the line:

We still need to find b, the y-intercept. To find this, we pick one of our points (either (–3,0) or (2,5)) and plug it into our equation. We'll use (–3,0).

Solve for b.

The equation is therefore written as .

The equation for a line takes the form where m is the slope and b is the y-intercept, where the graph hits the y-axis.

The y-intercept of this line is 1, so b=1.

We can figure out the slope by comparing how far the line goes up vs. how far it goes over between any 2 points. The two most obvious points on the graph are at and . Between these two points, the graph moves down 1 and over 5. This means the slope is , so we'll put that in for m.

The equation is then .

The equation for a line takes the form where m is the slope and b is the y-intercept, where the graph hits the y-axis.

The y-intercept of this line is -4, so b=-4.

We can figure out the slope by comparing how far the line goes up vs. how far it goes over between any 2 points. The two most obvious points on the graph are at  and . Between these two points, the graph moves up 3 and over 5. This means the slope is , so we'll put that in for m.

The equation is then .