All Algebra 1 Resources
Example Questions
Example Question #11 : How To Find F(X)
An infinite sequence begins as follows:
Assuming this pattern continues infinitely, what is the sum of the first one hundred terms?
This can be best solved by looking at this sum as follows:
with 
Example Question #13 : Algebraic Functions
Define 

Example Question #62 : Functions And Lines
Define 

What is 
Example Question #64 : Functions And Lines
Define 

What is 
Example Question #61 : Functions And Lines
Each of the four tables below defines a relationship between 

One of these tables does not define a function. Identified the table.
Table 3
Table 4
None of the above.
Table 2
Table 1
Table 3
In table 3 we see an 


Example Question #16 : Algebraic Functions
Each of the following 4 sets defines a relationship between 

A =
B=
C =
D =
Set A
Set A and Set B
Set B
Set C
Set D
Set A
Only in set A one can see that there is an unique value of 



Example Question #17 : Algebraic Functions
Which of the following equations does not represent a function?
The correct answer is equation D. If we solve for 
The fact that each value of 


Example Question #62 : Functions And Lines
Which of the following equations represents a one-to-one function:
Only equation B maps each value of 



Example Question #65 : Functions And Lines
Test whether the given function is symmetric with respect to the 

All of the above
y axis
x axis
origin
Not symmetric with respect to x axis, y axis, and the origin
Not symmetric with respect to x axis, y axis, and the origin
Since
It is not symmetric with respect the 
It is not symmetric with respect to the 
Hence multiplying by 
Hence it is not symmetric with respect to the origin.
Example Question #21 : How To Find F(X)
A function is defined by the following set of ordered pairs:
What is its inverse?
The function does not have an inverse.
The function does not have an inverse.
The inverse of a function is the relation that switches the positions of the coordinates of each ordered pair. However, for a function to have an inverse, the result of those switches must itself be a function. The switches yield the relation
which is not a function, since the 

All Algebra 1 Resources



























































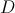




%5E%7B3%7D&space;-%5Cleft&space;(&space;-x&space;%5Cright&space;)%5E%7B2%7D&space;=&space;-x%5E%7B3%7D-x%5E%7B2%7D&space;%5Cneq&space;y)












