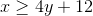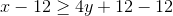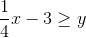We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Graphing

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Functions As Graphs

Which graph depicts a function?

Possible Answers:

Correct answer:

Explanation:

A function may only have one y-value for each x-value.

The vertical line test can be used to identify the function. If at any point on the graph, a straight vertical line intersects the curve at more than one point, the curve is not a function.

Report an Error

Example Question #1 : Functions As Graphs

The graph below is the graph of a piece-wise function in some interval. Identify, in interval notation, the decreasing interval.

Possible Answers:

$\left ( -\infty ,\infty \right )$

$(-\infty ,-2]\cup (-\infty ,1)\cup (1,3)$

$\left ( -\infty ,-2\right )\cup \left ( 1,3\right]$

$\left ( -\infty ,-2\right ]\cup \left ( 1,3 \right )$

$\left ( 1,3 \right )$

Correct answer:

$\left ( 1,3 \right )$

Explanation:

As is clear from the graph, in the interval between ( included) to , the f(x) is constant at and then from x=1 ( not included) to x=3 ( not included), the f(x) is a decreasing function.

Report an Error

Example Question #1 : How To Graph A Function

Which equation best represents the following graph?

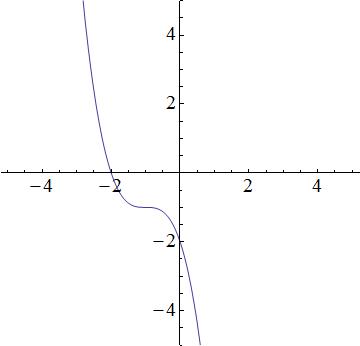
Graph6

Possible Answers:

$y(x)=e^{2x-1}+\frac{1}{9}$

None of these

y(x)=-(x+1)^2-1

y(x)=-(x+1)^3-1

y(x)=-x-1

Correct answer:

y(x)=-(x+1)^3-1

Explanation:

We have the following answer choices.

$y(x)=e^{2x-1}+\frac{1}{9}$

The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.

Report an Error

Example Question #1 : Solving Exponential Functions

What is the horizontal asymptote of the graph of the equation $y = -2e^{x-3} -5$ ?

Possible Answers:

y=5

y=-5

$y=-\frac{5}{2}$

y=3

y=-2

Correct answer:

y=-5

Explanation:

The asymptote of this equation can be found by observing that $e^{x-3} > 0$ regardless of . We are thus solving for the value of as $e^{x-3}$ approaches zero.

$-2e^{x-3} < -2\cdot 0$

$-2e^{x-3} < 0$

$-2e^{x-3} -5 < 0-5$

$-2e^{x-3} -5 < -5$

y<-5

So the value that cannot exceed is , and the line y = -5 is the asymptote.

Report an Error

Example Question #2 : Solving Exponential Functions

What is/are the asymptote(s) of the graph of the function

$f(x) = 5e^{x-2}-2$ ?

Possible Answers:

x=2

y = -2, x=-2

y = -2, x=2

y = -2

x=-2

Correct answer:

y = -2

Explanation:

An exponential equation of the form $f(x) = ae^{x-h} +k$ has only one asymptote - a horizontal one at y = k . In the given function, k = -2 , so its one and only asymptote is y = -2 .

Report an Error

Example Question #1 : How To Graph An Exponential Function

$\textup{What is the \textit{x}-intercept of the equation } y=e^{x-1}-1?$

Possible Answers:

$\textup{None of the above.}$

$-\infty$

$\textup{The graph does not intercept the \textit{x}-axis.}$

Correct answer:

Explanation:

$\\ \\ \textup{Solve the equation } \\0=e^{x-1} -1\\ e^{x-1}=1\\ {x-1}=\textup{ln}(1)=0\\ x=1.\\\textup{ Remember }e^0=1 \textup{, so when plugging } x=1 \textup{ in the initial equation, you obtain }\\ e^{1-1}-1=e^0-1=1-1=0.$

Report an Error

Example Question #1 : How To Graph A Two Step Inequality

Which graph depicts the following inequality?

$x\geq4y+12$

Possible Answers:

Question_12_incorrect_1

Question_12_incorrect_3

Question_12_correct

Question_12_incorrect_2

No real solution.

Correct answer:

Question_12_correct

Explanation:

Let's put the inequality in slope-intercept form to make it easier to graph:

$x\geq4y+12$

$x-12\geq4y+12-12$

$x-12\geq4y$

$\frac{x-12}{4}\geq\frac{4y}{y}$

$\frac{1}{4}x-3\geq y$

The inequality is now in slope-intercept form. Graph a line with slope $\frac{1}{4}$ and y-intercept .

Because the inequality sign is greater than or equal to, a solid line should be used.

Next, test a point. The origin 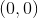(0,0) is good choice. Determine if the following statement is true:

$\frac{1}{4}(0)-3\geq0$

The statement is false. Therefore, the section of the graph that does not contain the origin should be shaded.

Report an Error

Example Question #2 : Parabolic Functions

What is the minimum possible value of the expression below?

$3x^{2}+6x-10$

Possible Answers:

The expression has no minimum value.

Correct answer:

Explanation:

We can determine the lowest possible value of the expression by finding the -coordinate of the vertex of the parabola graphed from the equation $y=3x^{2}+6x-10$ . This is done by rewriting the equation in vertex form.

$3x^{2}+6x-10$

$3(x^{2}+2x)-10$

$3(x^{2}+2x+1)-3* 1-10$

$3(x+1)^{2}-13$

The vertex of the parabola $y=3(x+1)^{2}-13$ is the point (-1, -13) .

The parabola is concave upward (its quadratic coefficient is positive), so represents the minimum value of . This is our answer.

Report an Error

Example Question #2 : Graphing Quadratic Functions

What is the vertex of the function $\small f(x)=2(x-4)^2+7$ ? Is it a maximum or minimum?

Possible Answers:

$\small (-4,7)$ ; maximum

$\small (4,7)$ ; minimum

$\small (-4,7)$ ; minimum

$\small (4,7)$ ; maximum

Correct answer:

$\small (4,7)$ ; minimum

Explanation:

The equation of a parabola can be written in vertex form: $\small f(x)=a(x-h)^2+k$ .

The point $\small (h,k)$ in this format is the vertex. If $\small a$ is a postive number the vertex is a minimum, and if $\small a$ is a negative number the vertex is a maximum.

$\small f(x)=2(x-4)^2+7$

In this example, $\small a=2$ . The positive value means the vertex is a minimum.

$\small h=4\ \text{and}\ k=7$

$\small (h,k)=(4,7)$

Report an Error

Example Question #1 : Graphing Polynomial Functions

Which of the graphs best represents the following function?

$f(x)=\frac{9}{10}x^2-7x+2$

Possible Answers:

Graph_line_

Graph_parabola_

Graph_exponential_

Graph_cube_

None of these

Correct answer:

Graph_parabola_

Explanation:

$f(x)=\frac{9}{10}x^2-7x+2$

The highest exponent of the variable term is two ( x^2 ). This tells that this function is quadratic, meaning that it is a parabola.

The graph below will be the answer, as it shows a parabolic curve.

Graph_parabola_

Report an Error

View Algebra Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View Algebra Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View Algebra Tutors

Dilip
Certified Tutor

University of Calcutta, Bachelor of Science, Physics. Indiana Institute of Technology, Master of Science, Physics.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Dallas Fort Worth, SSAT Tutors in Boston, SAT Tutors in San Diego, French Tutors in New York City, Calculus Tutors in Boston, English Tutors in Washington DC, ISEE Tutors in Atlanta, Reading Tutors in Phoenix, French Tutors in Boston, Statistics Tutors in Boston

Popular Courses & Classes

ACT Courses & Classes in Seattle, SSAT Courses & Classes in New York City, ACT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, ISEE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, GRE Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta

Popular Test Prep

GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in New York City, ACT Test Prep in Seattle, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in New York City, ISEE Test Prep in Dallas Fort Worth, SSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Houston, MCAT Test Prep in Boston, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Graphing

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : Functions As Graphs

Example Question #1 : Functions As Graphs

Example Question #1 : How To Graph A Function

Example Question #1 : Solving Exponential Functions

Example Question #2 : Solving Exponential Functions

Example Question #1 : How To Graph An Exponential Function

Example Question #1 : How To Graph A Two Step Inequality

Example Question #2 : Parabolic Functions

Example Question #2 : Graphing Quadratic Functions

Example Question #1 : Graphing Polynomial Functions

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: