We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Advanced Geometry : Trapezoids

Study concepts, example questions & explanations for Advanced Geometry

Create An Account

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : How To Find The Area Of A Trapezoid

Find the area of the figure below.

Possible Answers:

150.36

148.78

161.57

132.67

Correct answer:

161.57

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{7^2+12^2}=\sqrt{193}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(16+\sqrt{193})(8)=64+4\sqrt{193}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(7)(12)=42$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=64+4\sqrt{193}+42=161.57$

Make sure to round to places after the decimal.

Report an Error

Example Question #31 : How To Find The Area Of A Trapezoid

Find the area of the figure below.

Possible Answers:

50.67

55.30

62.12

59.38

Correct answer:

62.12

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{5^2+11^2}=\sqrt{146}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(11+\sqrt{146})(3)=\frac{33+3\sqrt{146}}{2}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(5)(11)=\frac{55}{2}$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=\frac{33+3\sqrt{146}}{2}+\frac{55}{2}=62.12$

Make sure to round to places after the decimal.

Report an Error

Example Question #33 : How To Find The Area Of A Trapezoid

Find the area of the figure below.

Possible Answers:

803.92

898.53

877.23

906.39

Correct answer:

898.53

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{22^2+26^2}=\sqrt{1160}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(34+\sqrt{1160})(18)=306+9\sqrt{1160}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(22)(26)=286$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=306+9\sqrt{1160}+286=898.53$

Make sure to round to places after the decimal.

Report an Error

Example Question #371 : Advanced Geometry

Find the area of the figure below.

Possible Answers:

150.81

140.58

131.95

136.01

Correct answer:

150.81

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{9^2+10^2}=\sqrt{181}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(13+\sqrt{181})(8)=52+4\sqrt{181}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(9)(10)=45$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=52+4\sqrt{181}+45=150.81$

Make sure to round to places after the decimal.

Report an Error

Example Question #31 : Trapezoids

Find the area of the figure.

Possible Answers:

91.85

94.37

103.37

111.73

Correct answer:

111.73

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{7^2+12^2}=\sqrt{193}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(14+\sqrt{193})(5)=35+\frac{5\sqrt{193}}{2}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(7)(12)=42$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=35+\frac{5\sqrt{117}}{2}+42=111.73$

Make sure to round to places after the decimal.

Report an Error

Example Question #32 : How To Find The Area Of A Trapezoid

Trapezoid

Figure NOT drawn to scale.

Examine the above trapezoid.

MN = 20 , TM = MP = 5 , RM = MA

True, false, or inconclusive: the area of Trapezoid TRAP is 200.

Possible Answers:

False

True

Correct answer:

True

Explanation:

The area of a trapezoid is equal to one half the product of half the height of the trapezoid and the sum of the lengths of the bases. This is

$A = \frac{1}{2} h (b_{1}+ b_{2})$

$A = \frac{1}{2} \cdot TP \cdot (TR + PA)$

or, equivalently,

$A = TP \cdot \frac{TR + PA}{2}$

The height of the trapezoid is

TP = TM + MP = 5 + 5 = 10 .

The lengths of bases $\overline{TR}$ and $\overline{PA}$ are not given, so it might appear that determining the area of the trapezoid is impossible.

However, it is given that TM = MP and RM = MA - that is, the segment $\overline{MN}$ bisects both legs of the trapezoid. This makes $\overline{MN}$ the midsegment of the trapezoid, the length of which is the arithmetic mean of those of the bases:

$MN = \frac{TR+ PA}{2}$ .

Therefore, the formula for the area of the trapezoid can be rewritten as

$A = TP \cdot MN$ ,

the product of the height and the length of the midsegment.

TP = 10 and MN = 20 , so

$A =10 \cdot 20 = 200$ ,

making the statement true.

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

What is the length of the diagonals of trapezoid ABCD ? Assume the figure is an isoceles trapezoid.

Trapezoid

Possible Answers:

$\sqrt{98}m$

$\sqrt{96}m$

$\sqrt{99}m$

$\sqrt{97}m$

$\sqrt{95}m$

Correct answer:

$\sqrt{97}m$

Explanation:

To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid ABCD :

Trapezoid

We know that the base of the triangle has length $9\: m$ . By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:

$12\: m - 6\: m = 6\: m$

Dividing by two, we have the length of each additional side on the bottom of the trapezoid:

$\frac{6\: m}{2} = 3\: m$

Adding these two values together, we get $9\: m$ .

The formula for the length of diagonal uses the Pythagoreon Theorem:

AC^2 = AE^2 + EC^2 , where is the point between and representing the base of the triangle.

Plugging in our values, we get:

$AC^2 = (9\: m)^2 + (4\: m)^2$

$AC^2 = 81\: m^2 + 16\: m^2$

$AC^2 = 97\: m^2$

$AC = \sqrt{97}\: m$

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Find the length of both diagonals of this quadrilateral.

Trapezoid 1

Possible Answers:

$\sqrt{97}, \sqrt{41}$

$\sqrt{97}, \sqrt{65}$

$\sqrt{85}, \sqrt{20}$

$\sqrt{41}, \sqrt{41}$

Correct answer:

$\sqrt{97}, \sqrt{65}$

Explanation:

All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:

Trapezoid solution 3

Using Pythagorean Theorem gives:

4^2 + 9^2 = C^2

16+81=C^2

97 = C^2 take the square root of each side

$\sqrt{97}= C$

Similarly, the other diagonal can be found with this right triangle:

Trapezoid solution 4

Once again using Pythagorean Theorem gives an answer of $\sqrt{65}$

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Find the length of the diagonals of this isosceles trapezoid, with $\textup{Height}=8$ .

Trapezoid 2

Possible Answers:

$\sqrt{73}$

$\sqrt{204}$

$\sqrt{128}$

$\sqrt{185}$

Correct answer:

$\sqrt{185}$

Explanation:

To find the length of the diagonals, split the top side into 3 sections as shown below:

Trapezoid solution 1

The two congruent sections plus 8 adds to 14. 14 - 8 = 6 , so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since 14-3=11 .

Trapezoid solution 2

We can solve for the diagonal, now pictured, using Pythagorean Theorem:

11^2 + 8^2 = C^2

121 + 64 = C^2

185 = C^2 take the square root of both sides

$\sqrt{185}=C$

Report an Error

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Find the length of the diagonal of the isosceles trapezoid given below.

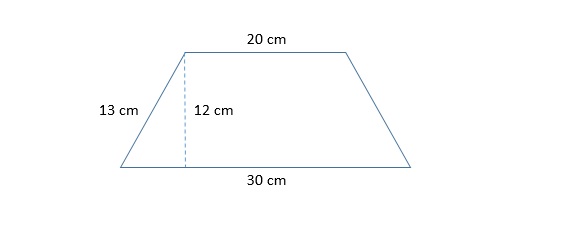
Trap1

Possible Answers:

$4\sqrt34\ cm$

$16\ cm$

$24\ cm$

$20\sqrt2\ cm$

Correct answer:

$4\sqrt34\ cm$

Explanation:

In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.

Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.

Trap2

$Using\ the\ pythagorean\ theorem\ we\ get: 12^2+20^2=diagonal^2$

$This\ simplifies\ to\ become\ 144+400=diagonal^2$

544=diagonal^2

We now take the square root of both sides:

$\sqrt544=\sqrt diagonal^2$

$\sqrt16*\sqrt34=diagonal$

$4\sqrt34=diagonal$

Report an Error

View Tutors

Adair
Certified Tutor

Marymount College, Bachelor of Science, Chemistry.

View Tutors

Paarth
Certified Tutor

New Jersey Institute of Technology, Bachelor of Science, Computer Science.

View Tutors

Joshua
Certified Tutor

Murray State University, Bachelor in Arts, Spanish. Lipscomb University, Bachelor of Science, Teacher Assistant.

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Houston, English Tutors in San Diego, Calculus Tutors in Denver, MCAT Tutors in Miami, Reading Tutors in Phoenix, SAT Tutors in Atlanta, Calculus Tutors in Dallas Fort Worth, GRE Tutors in Atlanta, GRE Tutors in Denver, SAT Tutors in Miami

Popular Courses & Classes

GRE Courses & Classes in Washington DC, ACT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Boston, ACT Courses & Classes in Los Angeles, Spanish Courses & Classes in Los Angeles, ISEE Courses & Classes in Boston, ACT Courses & Classes in Miami, GRE Courses & Classes in Boston, LSAT Courses & Classes in Chicago, SAT Courses & Classes in Philadelphia

Popular Test Prep

ISEE Test Prep in Miami, ISEE Test Prep in Houston, GMAT Test Prep in Houston, GRE Test Prep in San Diego, GRE Test Prep in Washington DC, GMAT Test Prep in New York City, SAT Test Prep in Houston, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Philadelphia, SAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Advanced Geometry : Trapezoids

Study concepts, example questions & explanations for Advanced Geometry

All Advanced Geometry Resources

Example Questions

Example Question #31 : How To Find The Area Of A Trapezoid

Example Question #31 : How To Find The Area Of A Trapezoid

Example Question #33 : How To Find The Area Of A Trapezoid

Example Question #371 : Advanced Geometry

Example Question #31 : Trapezoids

Example Question #32 : How To Find The Area Of A Trapezoid

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid

All Advanced Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: