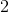Call Now to Set Up Tutoring:

(888) 888-0446

Advanced Geometry : How to find the area of a trapezoid

Study concepts, example questions & explanations for Advanced Geometry

Create An Account

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Quadrilaterals

A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?

Possible Answers:

$2\sqrt{2}$

$\sqrt{2}$

Correct answer:

Explanation:

In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:

area of trapezoid = (1/2)(4 + s)(s)

Similarly, the area of a square with sides of length a is given by a². Thus, the area of the square given in the problem is s².

We now can set the area of the trapezoid equal to the area of the square and solve for s.

(1/2)(4 + s)(s) = s²

Multiply both sides by 2 to eliminate the 1/2.

(4 + s)(s) = 2s²

Distribute the s on the left.

4s + s² = 2s²

Subtract s² from both sides.

4s = s²

Because s must be a positive number, we can divide both sides by s.

4 = s

This means the value of s must be 4.

The answer is 4.

Report an Error

Example Question #1 : Trapezoids

What is the area of this regular trapezoid?

Screen_shot_2013-03-18_at_3.27.27_pm

Possible Answers:

Correct answer:

Explanation:

To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.

Report an Error

Example Question #11 : How To Find The Area Of A Trapezoid

Trap

What is the area of the trapezoid above if a = 2, b = 6, and h = 4?

Possible Answers:

Correct answer:

Explanation:

Area of a Trapezoid = ½(a+b)*h

= ½ (2+6) * 4

= ½ (8) * 4

= 4 * 4 = 16

Report an Error

Example Question #1 : Trapezoids

Find the area of a trapezoid if the height is , and the small and large bases are and , respectively.

Possible Answers:

16x

6x^2

12x

12x^2

Correct answer:

6x^2

Explanation:

Write the formula to find the area of a trapezoid.

$A= \frac{1}{2} (b1+b2)h$

Substitute the givens and evaluate the area.

$A= \frac{1}{2} (b1+b2)h=\frac{1}{2} (2x+4x)(2x) = 2x^2+4x^2=6x^2$

Report an Error

Example Question #12 : How To Find The Area Of A Trapezoid

A right triangle and rectangle are placed adjacent to one another such that the composite figure formed by the triangle and rectangle is a trapezoid.

Find the area of the trapezoid given that the base of the triangle is 7 ft and the hypotenuse of the triangle is 25ft. The base of the rectangle is 9 feet.

Possible Answers:

$2880 ft^{2}$

$300ft^{2}$

$144ft^{2}$

$312.5 ft^{2}$

Correct answer:

$300ft^{2}$

Explanation:

$First\ we\ can\ find\ the\ height\ of\ the\ right\ triangle\ and\ assume\ that\ this\ is\ also\ the\ height\ of\ the\ rectangle\ and\ the\ trapezoid.$

$The\ height\ of\ the\ right\ triangle\ is\ obtained\ by\ using\ the\ Pythagorean\ theorem.$

$7^{2}+h^{2}=25^{2}$

$49+h^{2}=625$

$h^{2}=576$

h=24ft

$We\ know\ the\ top\ of\ the\ trapezoid\ is\ the\ same\ as\ the\ base\ of\ the\ rectangle\ which\ is\ 9\ cm.$

$We\ know\ that\ the\ base\ of\ the\ trapezoid\ is\ the\ sum\ of\ the\ base\ of\ the\ triangle\ and\ the\ base\ of\ the\ rectangle: 9+7=16$

$Now\ we\ have\ all\ parts\ needed\ to\ plug\ into\ the\ formula\ for\ the\ area\ of\ a\ trapezoid: A=\frac{b_{1}+b^{_{2}}}{2}*h$

$A=\frac{9+16}{2}*24=300cm^{2}$

Report an Error

Example Question #11 : How To Find The Area Of A Trapezoid

The average of the lengths of the top and bottom of trapezoid

ABCD is 15 cm.

What is the height of the trapezoid, if the area is $180 cm^{2}$ ?

Possible Answers:

6 cm

18 cm

12 cm

9 cm

Correct answer:

12 cm

Explanation:

$The\ area\ formula\ for\ a\ trapezoid\ is\ \frac{(b_{1}+b_{2})}2{}*h.$

$Adding\ the\ base\ and\ height\ and\ dividing\ by\ 2\ is\ the\ same\ as\ taking\ the\ average\ of\ the\ top\ and\ bottom.$ $So\ we\ can\ substitute\ 15\ cm\ for\ the\ \frac{(b_{1}+b_{2})}2{}\ portion\ of\ the\ formula.$ $We\ can\ set\ 15h=180\ and\ solve\ for\ h\ to\ get\ the\ height.$

$Divide\ both\ sides\ by\ 15\ to\ find\ that\ h=12cm.$

Report an Error

Example Question #13 : How To Find The Area Of A Trapezoid

What is the area of this trapezoid?

Screen shot 2015 10 21 at 3.29.16 pm

Possible Answers:

44.5

29.25

Correct answer:

29.25

Explanation:

The area of a trapezoid is

$A=\frac{1}{}2(b_{1}+b_{2})h$ .

In this particular case the known values are as follows.

$\\b_1=5 \\b_2=8 \\h=4.5$

Substituting in the given values into the area formula we arrive at the following solution.

$\frac{1}{2}(5+8)4.5=29.25$

Report an Error

Example Question #61 : Plane Geometry

$\small \small Find\ the\ height\ of\ a\ trapezoid\ with\ bases\ of\ 8\ and\ 12\ and\ an\ area\ of\ 80m^{2}.$

Possible Answers:

$\small 12\ m$

$\small 60\ m$

$\small \small \small 10\ m$

$\small \small 8\ m$

Correct answer:

$\small \small 8\ m$

Explanation:

$\small Use\ the\ area\ formula\ for\ a\ trapezoid.$

$\small A=\frac{b_{1}+b_{2}}2(h)$

$\small Substitute\ each\ known\ value\ then\ use\ algebra\ to\ solve\ for\ the\ height.$

$\small \small 80=\frac{8+12}{2}h$

$\small 80=10h$

$\small 8=h$

Report an Error

Example Question #352 : Advanced Geometry

Find the area of the trapezoid given below:

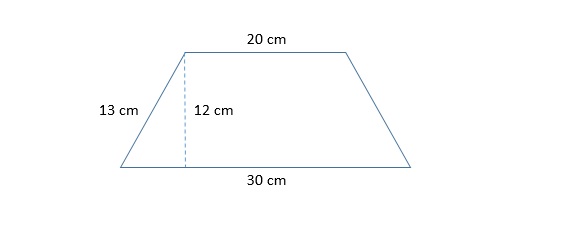
Trap1

Possible Answers:

$300\ cm^2$

$325\ cm^2$

$240\ cm^2$

$260\ cm^2$

Correct answer:

$300\ cm^2$

Explanation:

In order to find the area of a trapezoid, we must use the formula below:

$A=\frac{b_{1}+b_{2}}{2}(h)$

$In\ this\ trapezoid\ b_{1}=30\ and\ b_{2}=20.$

$We\ can\ also\ see\ that\ h=12.$

$When\ we\ plug\ in\ all\ of\ the\ above\ values\ into\ the\ formula\ we\ get:$

$A=\frac{20+30}{2}(12)$

A=300cm^2

Report an Error

Example Question #16 : Trapezoids

Show algebraically how to develop the trapezoid area formula.

Varsity7

Possible Answers:

$\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

$h(b_{1}\cdot b_{2})$

$= \frac{1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

$\frac{1}{2}(b_{1}+b_{2})+h$

$= \frac{h}{2}(b_{1}+b_{2})$

$\frac{1}{2}(b_{1}+b_{2})+h$ $\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{h}{2}(b_{1}+b_{2})$

$h^{2}(\frac{1}{2}b_{1}+\frac{1}{2}b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Correct answer:

$\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Explanation:

1) The area $A_{1}$ of the triangle that has base $b_{1}$ is $A_{1} = \frac{1}{2}(b_{1})h$ .

2) The area $A_{2}$ of the triangle that has base $b_{2}$ is $A_{2} = \frac{1}{2}(b_{2})h$ .

3) The sum of the two triangel areas is

$A_{1} + A_{2}$

$= \frac{1}{2}b_{1}h + \frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Report an Error

View Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View Tutors

Mudassara
Certified Tutor

CUNY College of Staten Island, Master of Arts, Business Administration and Management.

View Tutors

Shipra
Certified Tutor

Chaudhary Charan Singh University, India, Master's/Graduate, Commerce.

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Phoenix, Math Tutors in Atlanta, ISEE Tutors in Boston, Physics Tutors in Los Angeles, Calculus Tutors in Phoenix, LSAT Tutors in Boston, Biology Tutors in Houston, GRE Tutors in Atlanta, GRE Tutors in Philadelphia, Reading Tutors in Denver

Popular Courses & Classes

ISEE Courses & Classes in Boston, ISEE Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Boston, MCAT Courses & Classes in Atlanta, SSAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Philadelphia, GRE Courses & Classes in Miami, GRE Courses & Classes in Philadelphia, LSAT Courses & Classes in Houston, LSAT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in New York City, ISEE Test Prep in Chicago, GRE Test Prep in Philadelphia, SSAT Test Prep in Boston, GMAT Test Prep in Denver, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Phoenix, ACT Test Prep in Los Angeles, LSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Advanced Geometry : How to find the area of a trapezoid

Study concepts, example questions & explanations for Advanced Geometry

All Advanced Geometry Resources

Example Questions

Example Question #1 : Quadrilaterals

Example Question #1 : Trapezoids

Example Question #11 : How To Find The Area Of A Trapezoid

Example Question #1 : Trapezoids

Example Question #12 : How To Find The Area Of A Trapezoid

Example Question #11 : How To Find The Area Of A Trapezoid

Example Question #13 : How To Find The Area Of A Trapezoid

Example Question #61 : Plane Geometry

Example Question #352 : Advanced Geometry

Example Question #16 : Trapezoids

All Advanced Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: