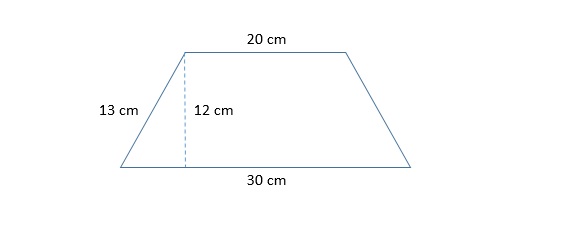
In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid. 

Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal. 

We now take the square root of both sides: 

1) The diagonal  can be found from  by using the Pythagorean Theorem.

2) The length of the base of ,  has to be found because  is the length of the base of .

3) .

4) Using the Pythagorean Theorem on  to find ,

5) Using the Pythagorean Theorem on  to find ,

To illustrate how to determine the correct length, draw a perpendicular segment from  to , calling the point of intersection .

 divides the trapezoid into Rectangle  and right triangle  .

Opposite sides of a rectangle are congruent, so .

. The two angles of a trapezoid along the same leg - in particular,  and  - are supplementary, so 

By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so , and

 is the hypotenuse of right triangle , so by the Pythagorean Theorem, its length can be calculated to be

Set  and :

To illustrate how to determine the correct length, draw a perpendicular segment from  to , calling the point of intersection .

 divides the trapezoid into Rectangle  and right triangle  .

Opposite sides of a rectangle are congruent, so .

. The two angles of a trapezoid along the same leg - in particular,  and  - are supplementary, so 

By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so , and

 is the hypotenuse of right triangle , so by the Pythagorean Theorem, its length can be calculated to be

Set  and :

To illustrate how to determine the correct length, draw a perpendicular segment from  to , calling the point of intersection .

 divides the trapezoid into Rectangle  and right triangle  .

Opposite sides of a rectangle are congruent, so .

. The two angles of a trapezoid along the same leg - in particular,  and  - are supplementary, so 

By the 45-45-45 Triangle Theorem,

and

 is the hypotenuse of right triangle , so by the Pythagorean Theorem, its length can be calculated to be

Set  and :

A rhombus is a four-sided figure where all sides are straight and equal in length. All opposite sides are parallel. A square is considered to be a rhombus.

Solving for the area of rhombus  requires knowledge of the equation for finding the area of a rhombus. The equation is , where  and  are the two diagonals of the rhombus. Since both of these values are given to us in the original problem, we merely need to substitute these values into the equation to obtain:

The area of rhombus  is therefore  square units. 

The formula for the area of a rhombus from the diagonals is half the product of the diagonals, or in mathematical terms:

 where  and  are the lengths of the diagonals.

Substituting our values yields, 

One of the formulas for a rhombus is base times height,

Since a rhombas has equal sides, the base is 5 and the height of the rhombus is the same as the height of the rectangle, 4.

Substituting in these values we get the following:

To solve for the area of the rhombus , we must use the equation , where  and  are the diagonals of the rhombus. Since the perimeter of the rhombus is , and by definition all 4 sides of a rhombus have the same length, we know that the length of each side is . We can find the length of the other diagonal if we recognize that the two diagonals combined with a side edge form a right triangle. The length of the hypotenuse is , and each leg of the triangle is equal to one-half of each diagonal. We can therefore set up an equation involving Pythagorean's Theorem as follows:

, where  is equal to one-half the length of the unknown diagonal.

We can therefore solve for  as follows:

 is therefore equal to 8, and our other diagonal is 16. We can now use both diagonals to solve for the area of the rhombus:

The area of rhombus  is therefore equal to