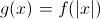f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.

Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).

The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.

The three transformations of f(x) can be represented as –f(x + 4) – 5.

The answer is –f(x + 4) – 5.

A reflection over the line  involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).

The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:

The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so

When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a). 

Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2). 

Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.

First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x₁, y₁) and (x₂, y₂).

slope = (2 – (–4))/(–6 –3)

= 6/–9 = –2/3

Next, we can use the point-slope formula to find the equation for q.

y – y₁ = slope(x – x₁)

y – 2 = (–2/3)(x – (–6))

Multiply both sides by 3.

3(y – 2) = –2(x + 6)

3y – 6 = –2x – 12

Add 2x to both sides.

2x + 3y – 6 = –12

Add six to both sides.

2x + 3y = –6

The answer is 2x + 3y = –6.

This quadratic is presented in vertex form. 

First, the negative sign will reflect the graph over the x-axis, if the negative sign were inside the parentheses it would be reflected over the y-axis. 

Second, the 2 will stretch the graph vertically, if the 2 had been inside the parentheses that would have been a horizontal shrink. 

Third, the 5 inside the parentheses, translates the graph 5 spaces right because we are plugging in a positive 5 into the original vertex form for "h". A negative 5 would change the sign inside the parentheses. 

Finally, the 4 outside the parentheses is the k-value, which translates the graph up 4 spaces in this case. 

If the function is reflected over the x-axis, then .

It will be the opposite of what is currently written.

Therefore, 

becomes 

.

When a function is reflected over the y-axis, . 

becomes 

which is simplifed as 

.

In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding. 

Therefore, g(x) = f(–x).

f(x) = x³ – 2x² + x – 4

g(x) = f(–x) = (–x)³ – 2(–x)² + (–x) + 4

g(x) = (–1)³x³ –2(–1)²x² – x + 4

g(x) = –x³ –2x² –x + 4.

The answer is –x³ –2x² –x + 4.

The period is the time it takes for the graph to complete one cycle.

In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches .

Therefore, the period is