We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Advanced Geometry : Advanced Geometry

Study concepts, example questions & explanations for Advanced Geometry

Create An Account

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Graphing

Solve and graph the following inequality:

$2x - 7 \geq 6$

Possible Answers:

$x\geq13$

$x\geq6.5$

$x\leq 13$

x=6.5

$x\leq6.5$

Correct answer:

$x\geq6.5$

Explanation:

To solve the inequality, the first step is to add to both sides:

$2x - 7 +7 \geq 6+7$

$2x \geq 13$

The second step is to divide both sides by :

$\frac{2x}{2} \geq \frac{13}{2}$

$x \geq 6.5$

To graph the inequality, you draw a straight number line. Fill in the numbers from 6.5 to infinity. Infinity can be designated by a ray. Be sure to fill in the number 6.5 , since the equation indicated greater than OR equal to.

The graph should look like:

Number_line

Report an Error

Example Question #201 : Coordinate Geometry

Points (3,0) and (0,3) lie on a circle. Which of the following could be the equation of that circle?

Possible Answers:

$(x-3)^{2}+(y+3)^{2}=3$

$(x+3)^{2}+(y+3)^{2}=9$

$(x-3)^{2}+(y+3)^{2}=9$

$(x-3)^{2}+(y-3)^{2}=3$

$(x-3)^{2}+(y-3)^{2}=9$

Correct answer:

$(x-3)^{2}+(y-3)^{2}=9$

Explanation:

If we plug the points (3,0) and (0,3) into each equation, we find that these points work only in the equation $(x-3)^{2}+(y-3)^{2}=9$ . This circle has a radius of and is centered at (3,3) .

Report an Error

Example Question #1 : Graphing

Which of the following lines is perpendicular to the line y=3x+4 ?

Possible Answers:

$y=\frac{x}{3}+4$

$y=\frac{x}{3}+3$

$y=\frac{-x}{3}+2$

y=3x+6

y=3x+2

Correct answer:

$y=\frac{-x}{3}+2$

Explanation:

The key here is to look for the line whose slope is the negative reciprocal of the original slope.

In this case, $\frac{-1}{3}$ is the negative reciprocal of .

Therefore, the equation of the line which is perpendicular to the original equation is:

$y=\frac{-x}{3}+2$

Report an Error

Example Question #1 : How To Graph A Two Step Inequality

Which inequality does this graph represent?

Inequality a

Possible Answers:

$0\geq y \geq -\frac{3}{5}x+3$ ;

$0 \geq y \geq \frac{1}{2}+1$

$0<y\leq-\frac{1}{2}x+1$ ;

$0<y\leq \frac{3}{5}x+3$

$-\frac{3}{5}x+3 \geq y \geq \frac{1}{2}x+1$

$0<y\leq \frac{1}{2}x+1$ ;

$0<y\leq-\frac{3}{5}x+3$

Correct answer:

$0<y\leq \frac{1}{2}x+1$ ;

$0<y\leq-\frac{3}{5}x+3$

Explanation:

The two lines represented are $y=\frac{1}{2}x+1$ and $y=-\frac{3}5{}x+3$ . The shaded region is below both lines but above y=0.

Report an Error

Example Question #1 : How To Graph A Two Step Inequality

What is the area of the shaded region for the following inequality:

$y\leq -\frac{3}{5}x+3$ ;

$0\leq y \leq \frac{1}{2}x+1$

Possible Answers:

7.5

5.2

0.5

Correct answer:

Explanation:

This inequality will produce the following graph:

Inequality a

The shaded area is a triangle with base 7 and height 2.

To find the area, plug these values into the area formula for a triangle, $\frac{1}{2}bh$ .

In this case, we are evaluating $\frac{1}{2}\cdot 7\cdot 2$ , which equals 7.

Report an Error

Example Question #291 : Advanced Geometry

What is the area of the shaded region for this system of inequalities:

$0\leq y \leq \frac{1}{2}x+3$ ; $\frac{1}{2}x \leq y \leq 5$

Possible Answers:

$\infty$

Correct answer:

Explanation:

Once graphed, the inequality will look like this:

Inequality b

To find the area, it is easiest to consider it as 2 congruent triangles with base 6 and height 3.

The total area will then be

$2\cdot \frac{1}{2}(6)(3)$ , or just $6\cdot 3 = 18$ .

Report an Error

Example Question #1 : How To Graph A Two Step Inequality

Find the -intercept for the following:

3x-2y=11

Possible Answers:

$\left (0,\frac{-11}{2} \right )$

$\left (0,-2 \right )$

$\left (0,\frac{11}{2} \right )$

$\left (0,2 \right )$

Correct answer:

$\left (0,\frac{-11}{2} \right )$

Explanation:

$When\ finding\ the\ y-intercept,\ you\ must\ plug\ in\ x=0\ and\ solve\ for\ y.$

$When\ x=0\ the\ equation\ becomes: 3(0)-2y=11$ .

$The\ next\ step\ becomes: -2y=11$ .

$Dividing\ both\ sides\ by\ -2\ gives\ us\ the\ y-int\ which\ is\ y=-\frac{11}{2}$ .

Report an Error

Example Question #201 : Graphing

Let D be the region on the (x,y) coordinate plane that contains the solutions to the following inequalities:

$x\leq k$ , where is a positive constant

$0\leq y\leq 12x$

Which of the following expressions, in terms of , is equivalent to the area of D?

Possible Answers:

12k^2

3k^2

8k^2

6k^2

4k^2

Correct answer:

6k^2

Explanation:

Inequality_region1

Report an Error

Example Question #1 : Kites

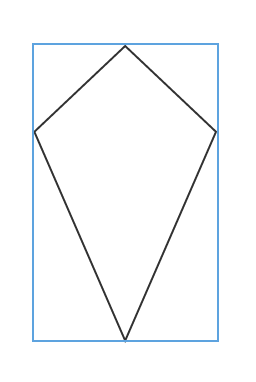
Screen_shot_2015-03-06_at_6.20.29_pm

The area of the rectangle is , what is the area of the kite?

Possible Answers:

Correct answer:

Explanation:

The area of a kite is half the product of the diagonals.

$A=\frac{p \cdot q}{2}$

The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.

Therefore our equation becomes:

$A=\frac{l \cdot w}{2}$ .

We also know the area of the rectangle is $A=l \cdot w=80$ . Substituting this value in we get the following:

$A=\frac{l \cdot w}{2}=\frac{80}{2}=40$

Thus,, the area of the kite is .

Report an Error

Example Question #1 : Kites

Given: Quadrilateral KITE such that $\overline{KI} \cong \overline{KE}$ , $\overline{TI} \cong \overline{TE}$ , $m \angle K = 60^{\circ }$ , $\angle T$ is a right angle, and diagonal $\overline{I E}$ has length 24.

Give the length of diagonal $\overline{KT}$ .

Possible Answers:

None of the other responses is correct.

$12+ 12\sqrt{3}$

$12+ 12\sqrt{2}$

$12\sqrt{2}+ 12\sqrt{3}$

Correct answer:

$12+ 12\sqrt{3}$

Explanation:

The Quadrilateral KITE is shown below with its diagonals $\overline{I E}$ and $\overline{KT}$ .

. We call the point of intersection :

Kite

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, $\overline{KT}$ bisects the $60 ^{\circ }$ and $90^{\circ }$ angles of the kite. Consequently, $\bigtriangleup KXI$ is a 30-60-90 triangle and $\bigtriangleup TXI$ is a 45-45-90 triangle. Also, the diagonal that connects the common vertices of the pairs of adjacent sides bisects the other diagonal, making the midpoint of $\overline{IE}$ . Therefore,

$IX = \frac{1}{2} \cdot IE = \frac{1}{2} \cdot 24 = 12$ .

By the 30-60-90 Theorem, since $\overline{IX}$ and $\overline{KX}$ are the short and long legs of $\bigtriangleup KXI$ ,

$KX = IX \cdot \sqrt{3}= 12 \sqrt{3}$

By the 45-45-90 Theorem, since $\overline{IX}$ and $\overline{XT}$ are the legs of a 45-45-90 Theorem,

XT = IX = 12 .

The diagonal $\overline{KT}$ has length

$KT =XT + KX= 12+ 12\sqrt{3}$ .

Report an Error

View Tutors

Pamela
Certified Tutor

Florida International University, Bachelor in Arts, Psychology.

View Tutors

Nicholas
Certified Tutor

University of St Thomas, Current Undergrad Student, Physics.

View Tutors

Beth Ann
Certified Tutor

Missouri State University-Springfield, Bachelor in Arts, English. William Woods University, Master of Arts, Elementary School...

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Phoenix, Reading Tutors in Phoenix, Chemistry Tutors in Atlanta, GMAT Tutors in Boston, LSAT Tutors in New York City, Algebra Tutors in Los Angeles, Computer Science Tutors in Denver, French Tutors in Washington DC, Physics Tutors in Dallas Fort Worth, Statistics Tutors in Los Angeles

Popular Courses & Classes

ACT Courses & Classes in Miami, GRE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Houston, SAT Courses & Classes in Miami, MCAT Courses & Classes in Seattle, LSAT Courses & Classes in New York City, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in Phoenix, GRE Courses & Classes in Miami, Spanish Courses & Classes in Washington DC

Popular Test Prep

MCAT Test Prep in Miami, SSAT Test Prep in Miami, LSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Washington DC, MCAT Test Prep in San Diego, ACT Test Prep in Chicago, GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in Atlanta, MCAT Test Prep in Atlanta, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Advanced Geometry : Advanced Geometry

Study concepts, example questions & explanations for Advanced Geometry

All Advanced Geometry Resources

Example Questions

Example Question #1 : Graphing

Example Question #201 : Coordinate Geometry

Example Question #1 : Graphing

Example Question #1 : How To Graph A Two Step Inequality

Example Question #1 : How To Graph A Two Step Inequality

Example Question #291 : Advanced Geometry

Example Question #1 : How To Graph A Two Step Inequality

Example Question #201 : Graphing

Example Question #1 : Kites

Example Question #1 : Kites

All Advanced Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: