The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.

Millikin used an experimental setup like the one shown in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.

Figure 1

By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.

Using this information, Millikin was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified. 

Figure 2

When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation: 

Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.

Table 1

A stronger electric field is needed to keep the oil drop in the field when a vacuum is used. This is most likely due to:

A student performed the following procedures to study various photosynthetic pigments (light-absorbing chemicals) in tree leaves and the wavelengths of light they absorb.

Experiment 1:

The student obtained samples of leaves from oaks, maples, ashes, sycamores, and poplars. Each leaf sample was ground separately with a mortar and pestle to release the pigments, and then each sample was suspended in water to make a colored solution of the pigment. The student then measured the absorption spectrum (a graph of how much light is absorbed by a pigment at varying wavelengths of light) of each solution in a device called a spectrophotometer. The setup of a spectrophotometer is shown below in Diagram 1.

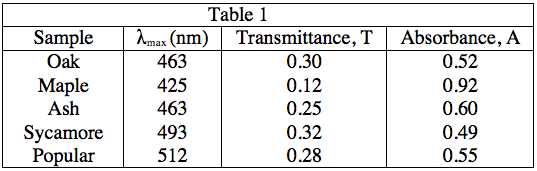
The light source emits white light, which is split into its various wavelengths by the prism. Next, a slit, which can be moved up or down to select a particular wavelength, is used to transmit just a single wavelength to the sample. The sample absorbs a fraction of this light that is characteristic to the pigment in the sample, and the rest is transmitted to the detector for a readout. Using the spectrophotometer, the student found the λ_max (the wavelength of light in nanometers (nm) that the pigment absorbs most intensely, for each sample) and recorded the results in Table 1. Table 1 also shows the transmittance and absorbance values at λ_max. Transmittance, T, is defined as the fraction of light, expressed as a decimal, which passes through the sample. Absorbance, A, is given by:

                                    A = –log(T)   or  10^–A = T

Experiment 2:

A student is given a leaf from an unknown source. She crushes and extracts the pigment according to the procedure in Experiment 1. Measuring the absorbance spectrum in the spectrophotometer produces the following readout, shown in Diagram 2.

                                                     Diagram 2

A lumberjack wants to plant trees that make the most efficient use of sunlight in a shady area of her land. Which trees should she plant?

A student performed the following procedures to study various photosynthetic pigments (light-absorbing chemicals) in tree leaves and the wavelengths of light they absorb.

Experiment 1:

The student obtained samples of leaves from oaks, maples, ashes, sycamores, and poplars. Each leaf sample was ground separately with a mortar and pestle to release the pigments, and then each sample was suspended in water to make a colored solution of the pigment. The student then measured the absorption spectrum (a graph of how much light is absorbed by a pigment at varying wavelengths of light) of each solution in a device called a spectrophotometer. The setup of a spectrophotometer is shown below in Diagram 1.

The light source emits white light, which is split into its various wavelengths by the prism. Next, a slit, which can be moved up or down to select a particular wavelength, is used to transmit just a single wavelength to the sample. The sample absorbs a fraction of this light that is characteristic to the pigment in the sample, and the rest is transmitted to the detector for a readout. Using the spectrophotometer, the student found the λ_max (the wavelength of light in nanometers (nm) that the pigment absorbs most intensely, for each sample) and recorded the results in Table 1. Table 1 also shows the transmittance and absorbance values at λ_max. Transmittance, T, is defined as the fraction of light, expressed as a decimal, which passes through the sample. Absorbance, A, is given by:

                                    A = –log(T)   or  10^–A = T

Experiment 2:

A student is given a leaf from an unknown source. She crushes and extracts the pigment according to the procedure in Experiment 1. Measuring the absorbance spectrum in the spectrophotometer produces the following readout, shown in Diagram 2.

                                                Diagram 2

In Experiment 2, at which of the following wavelengths, in nanometers, is the most amount of light transmitted through the sample?

A student performed the following procedures to study various photosynthetic pigments (light-absorbing chemicals) in tree leaves and the wavelengths of light they absorb.

Experiment 1:

The student obtained samples of leaves from oaks, maples, ashes, sycamores, and poplars. Each leaf sample was ground separately with a mortar and pestle to release the pigments, and then each sample was suspended in water to make a colored solution of the pigment. The student then measured the absorption spectrum (a graph of how much light is absorbed by a pigment at varying wavelengths of light) of each solution in a device called a spectrophotometer. The setup of a spectrophotometer is shown below in Diagram 1.

The light source emits white light, which is split into its various wavelengths by the prism. Next, a slit, which can be moved up or down to select a particular wavelength, is used to transmit just a single wavelength to the sample. The sample absorbs a fraction of this light that is characteristic to the pigment in the sample, and the rest is transmitted to the detector for a readout. Using the spectrophotometer, the student found the λ_max (the wavelength of light in nanometers (nm) that the pigment absorbs most intensely, for each sample) and recorded the results in Table 1. Table 1 also shows the transmittance and absorbance values at λ_max. Transmittance, T, is defined as the fraction of light, expressed as a decimal, which passes through the sample. Absorbance, A, is given by:

                                    A = –log(T)   or  10^–A = T

Experiment 2:

A student is given a leaf from an unknown source. She crushes and extracts the pigment according to the procedure in Experiment 1. Measuring the absorbance spectrum in the spectrophotometer produces the following readout, shown in Diagram 2.

                                                     Diagram 2

A standardized sample of a pigment often found in plant leaves, called Chlorophyll A, was placed into the spectrophotometer and found to have a λ_maxof 425 nm. The leaves of which tree most likely have a high concentration of Chlorophyll A?

A student wanted to study the kinetics, or rates of a chemical reaction based on the concentrations of its reactants and products, of the reaction shown below.

This reaction is easy to monitor using a spectrophotometer, which measures how much light of a particular wavelength is absorbed by a solution. The deep purple potassium permanganate, or , absorbs light of a 550 nm wavelength in proportion to its concentration in the reaction solution. Manganese sulfate, or , is pale pink and absorbs light of a 500 nm wavelength in proportion to its concentration in the reaction solution. All other reactants and products are colorless and do not absorb visible light and thus cannot be monitored using the spectrophotometer.

Experiment 1:

The student constructed a standard curve, or a graph of the absorbance of solutions of varying concentrations of potassium permanganate, to quantify the relationship between concentration and absorbance. To prepare five sample of increasing concentration, he labeled five test tubes A, B, C, D, and E, weighed out 0.1, 0.2, 0.3, 0.4, and 0.5 grams of potassium permanganate into each, respectively, and added 1 milliliter (mL) of water to each test tube to dissolve. Then, he used the spectrophotometer to determine the absorbance at 550 nm of each sample. The data is graphed in Figure 1 below.

                                                        Figure 1

Experiment 2: 

The student then studied potassium permanganate in the presence of oxalic acid, , to observe the reaction. Monitoring both the absorbances of potassium permanganate and manganese sulfate, he was able to determine the reaction rate using a special setting on the spectrophotometer. The reaction rate at various concentrations of reactants is shown below in Table 1.

The rate constant, , for a chemical reaction involving two reactants is given by the following equation: 

What is the rate constant for the reaction studied in Experiment 2?

A student wanted to study the kinetics, or rates of a chemical reaction based on the concentrations of its reactants and products, of the reaction shown below.

This reaction is easy to monitor using a spectrophotometer, which measures how much light of a particular wavelength is absorbed by a solution. The deep purple potassium permanganate, or , absorbs light of a 550 nm wavelength in proportion to its concentration in the reaction solution. Manganese sulfate, or , is pale pink and absorbs light of a 500 nm wavelength in proportion to its concentration in the reaction solution. All other reactants and products are colorless and do not absorb visible light and thus cannot be monitored using the spectrophotometer.

Experiment 1:

The student constructed a standard curve, or a graph of the absorbance of solutions of varying concentrations of potassium permanganate, to quantify the relationship between concentration and absorbance. To prepare five sample of increasing concentration, he labeled five test tubes A, B, C, D, and E, weighed out 0.1, 0.2, 0.3, 0.4, and 0.5 grams of potassium permanganate into each, respectively, and added 1 milliliter (mL) of water to each test tube to dissolve. Then, he used the spectrophotometer to determine the absorbance at 550 nm of each sample. The data is graphed in Figure 1 below.

                                                        Figure 1

Experiment 2: 

The student then studied potassium permanganate in the presence of oxalic acid, , to observe the reaction. Monitoring both the absorbances of potassium permanganate and manganese sulfate, he was able to determine the reaction rate using a special setting on the spectrophotometer. The reaction rate at various concentrations of reactants is shown below in Table 1.

Reaction rate is given by the following equation:

Imagine that  for this particular reaction. If a student uses concentrations of 2.0 grams/mL for both of the reactants, what should he expect the rate to be?

The Ideal Gas Law is as follows:

 is pressure as measured in Pascals,  is volume as measured in cubic meters,  is the number of moles of the gas,  is the gas constant known as 8.314 Joules per mole times Kelvin, and  is the temperature measured in Kelvin.

A class of students began studying the Ideal Gas Law and how the Pressure and the Volume relate to one another.  They took 20 moles of a sample gas and kept the room at a temperature of 300 Kelvin.  They then used different sized containers of the gas to limit and expand the volume.  At each different volume, they measure the pressure of the gas on its container.  The table they made from their results is seen in table 1.

TABLE 1 

And they graph their findings in Figure 1.

FIGURE 1

If the Kelvin temperature were to rise, what would happen to the pressure?

The Ideal Gas Law is as follows:

 is pressure as measured in Pascals,  is volume as measured in cubic meters,  is the number of moles of the gas,  is the gas constant known as 8.314 Joules per mole times Kelvin, and  is the temperature measured in Kelvin.

A class of students began studying the Ideal Gas Law and how the Pressure and the Volume relate to one another. They took 20 moles of a sample gas and kept the room at a temperature of 300 Kelvin. They then used different sized containers of the gas to limit and expand the volume. At each different volume, they measure the pressure of the gas on its container. The table they made from their results is seen in table 1.

TABLE 1 

And they graph their findings in Figure 1.

FIGURE 1

Would Figure 1 be the same for 1 mole of hydrogen gas as it would be for 1 mole of oxygen gas?

The Ideal Gas Law is as follows:

 is pressure as measured in Pascals,  is volume as measured in cubic meters,  is the number of moles of the gas,  is the gas constant known as 8.314 Joules per mole times Kelvin, and  is the temperature measured in Kelvin.

A class of students began studying the Ideal Gas Law and how the Pressure and the Volume relate to one another. They took 20 moles of a sample gas and kept the room at a temperature of 300 Kelvin. They then used different sized containers of the gas to limit and expand the volume. At each different volume, they measure the pressure of the gas on its container. The table they made from their results is seen in table 1.

TABLE 1 

And they graph their findings in Figure 1.

FIGURE 1

What would the pressure be if the volume was 100 cubic meters?

The Ideal Gas Law is as follows:

 is pressure as measured in Pascals,  is volume as measured in cubic meters,  is the number of moles of the gas,  is the gas constant known as 8.314 Joules per mole times Kelvin, and  is the temperature measured in Kelvin.

A class of students began studying the Ideal Gas Law and how the Pressure and the Volume relate to one another.  They took 20 moles of a sample gas and kept the room at a temperature of 300 Kelvin.  They then used different sized containers of the gas to limit and expand the volume.  At each different volume, they measure the pressure of the gas on its container.  The table they made from their results is seen in table 1.

TABLE 1 

And they graph their findings in Figure 1.

FIGURE 1

If the same 20 moles of the same gas were taken to sea level (at a pressure of 100,000 Pascals) and heated to 300 Kelvin, how large would the volume of the container be to hold it at its new pressure?