ACT Math : Cosine
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : Cosine
In the above triangle, 
With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.
Example Question #1 : How To Find An Angle With Cosine
For the above triangle, 
With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.
Example Question #2 : How To Find An Angle With Cosine
For the above triangle, 
This triangle cannot exist.
This triangle cannot exist.
With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. However, if we plug the given values into the formula for cosine, we get:
This problem does not have a solution. The sides of a right triangle must be shorter than the hypotenuse. A triangle with a side longer than the hypotenuse cannot exist. Similarly, the domain of the arccos function is 
Example Question #1 : How To Find An Angle With Cosine
A 
You can draw your scenario using the following right triangle:
Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:
Example Question #1 : Cosine
What is the value of 
Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:
Example Question #1 : How To Find An Angle With Cosine
A support beam (buttress) lies against a building under construction. If the beam is 
Our answer lies in inverse functions. If the buttress is 
Thus, using inverse functions we can say that
Thus, our buttress strikes the buliding at approximately a 
Example Question #1 : How To Find An Angle With Cosine
A stone monument stands as a tourist attraction. A tourist wants to catch the sun at just the right angle to "sit" on top of the pillar. The tourist lies down on the ground 
Our answer lies in inverse functions. If the monument is 
Thus, using inverse functions we can say that
Thus, our buttress strikes the buliding at approximately a 
Example Question #3 : Cosine
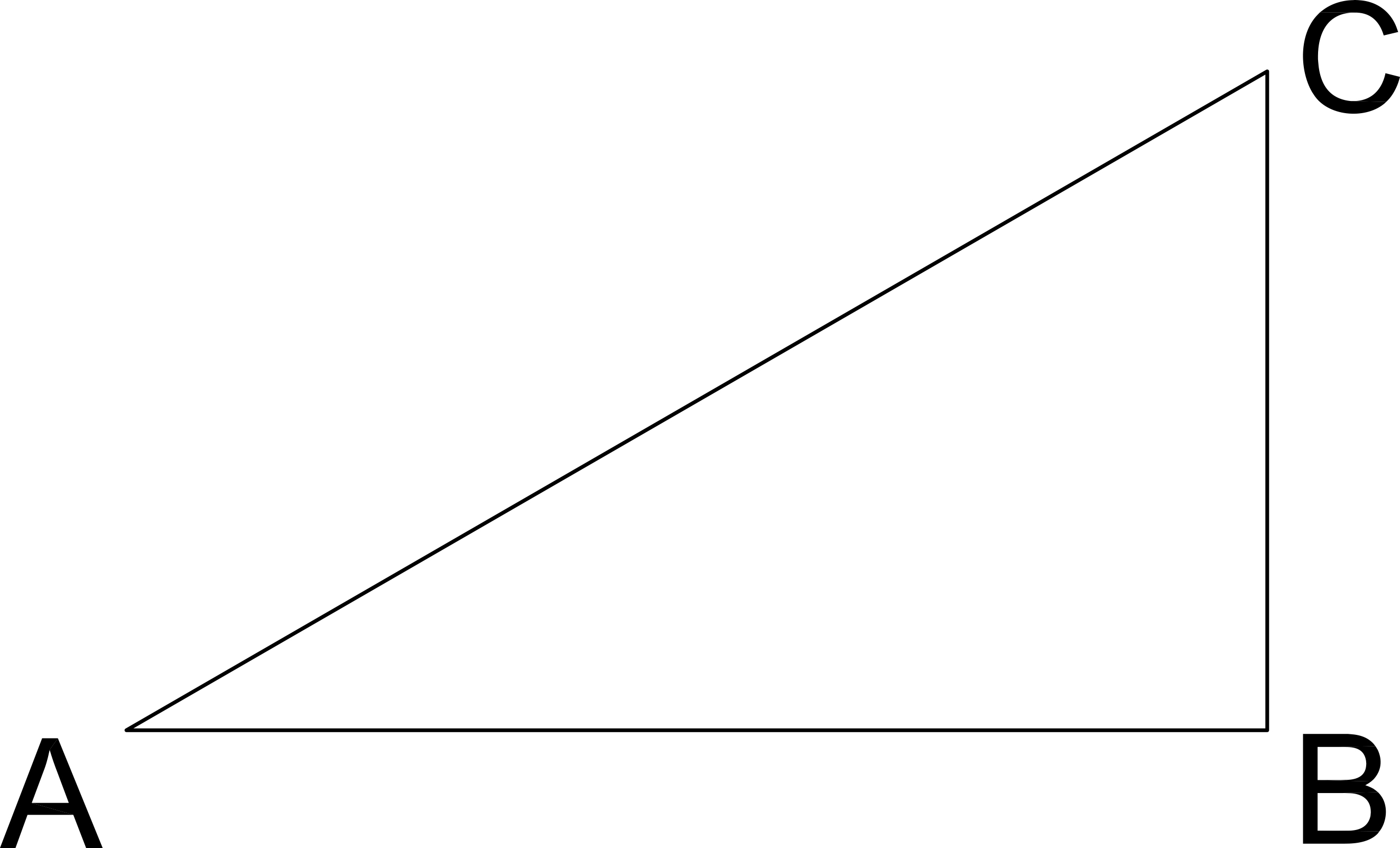
If angle A measures 30 degrees and the hypotenuse is 4, what is the length of AB in the given right triangle?
2√3
4
8√3
2
√3
2√3
Cosine A = Adjacent / Hypotenuse = AB / AC = AB / 4
Cosine A = AB / 4
Cos (30º) = √3 / 2 = AB / 4
Solve for AB
√3 / 2 = AB / 4
AB = 4 * (√3 / 2) = 2√3
Example Question #1 : Cosine
To solve this problem you need to make the triangle that the problem is talking about. Cosine is equal to the adjacent side over the hypotenuse of a right triangle
So this is what our triangle looks like:
Now use the pythagorean theorem to find the other side:
Sine is equal to the opposite side over the hypotenuse, the opposite side is 12
Example Question #1 : How To Find A Missing Side With Cosine
The hypotenuse of right triangle HLM shown below is 
Remember that
Then, we can set up the equation using the given information.
Now, solve for 
Certified Tutor
All ACT Math Resources
