All ACT Math Resources
Example Questions
Example Question #2 : How To Find A Missing Side With Cosine

What is 
Recall that the cosine of an angle is the ratio of the adjacent side to the hypotenuse of that triangle. Thus, for this triangle, we can say:
Solving for 

Example Question #3 : How To Find A Missing Side With Cosine
A man has a rope that is 

Begin by drawing out this scenario using a little right triangle:

We know that the cosine of an angle is equal to the ratio of the side adjacent to that angle to the hypotenuse of the triangle. Thus, for our triangle, we know:
Using your calculator, solve for 
This is 
Thus, rounded, your answer is 

Example Question #4 : How To Find A Missing Side With Cosine

In the right triangle shown above, what is the 
Use SOH-CAH-TOA to solve for the sine of a given angle. This stands for:

From our triangle we see that at point 



Example Question #5 : How To Find A Missing Side With Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 




Thus, 
Example Question #1 : How To Find A Missing Side With Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 




Thus, 
Example Question #7 : How To Find A Missing Side With Cosine
An airline pilot must know the exact vertical height of his plane above the runway to know when to extend the landing gear under the nose. If the nose of the plane is 


(Ignore the height of the plane itself).
The plane itself is effectively at the top of a right triangle, with topmost angle 


Now, solve for the adjacent:
Thus, our plane's nose is approximately 
Example Question #8 : How To Find A Missing Side With Cosine
Edgar is standing at the top of a 35-foot long slide. He knows that the angle between the top of the slide and the ladder that he climbed to reach the top is 68 degrees. If the ladder meets the ground at a right angle, how far did Edgar climb?
Edgar is standing on top of a right triangle because the angle from the vertical ladder to the ground is 90 degrees. To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.
In order to solve for the missing side, you need to choose the trigonometric function that includes the side you need to find and the side that you know, relative to the angle that you know. In this case, you know the hypotenuse, so you would not use the tangent function; furthermore, you are looking for the side that is adjacent to the 68-degree angle. Thus, you need the function that incorporates adjacent and hypotenuse—the cosine function.
Typically, you would use a calculator at this point to calculate the cosine function; however, based on the answer choices provided, you can stop at this point.
Example Question #11 : Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 


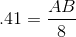

Thus, 
Example Question #11 : Cosine
What is the domain of 
Does not exist.
The domain of a function is referring to the x values that can be plugged into the function and produce a value.
The domain of the parent function 
The 
Therefore, the answer is 
Example Question #111 : Trigonometry
Given a function 
The function 

The domain of the parent function is 


The answer is 
Certified Tutor
Certified Tutor
All ACT Math Resources



























































![(-\infty,-3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/303613/gif.latex)

![[-3,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/303611/gif.latex)

![[2,6]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/315532/gif.latex)







