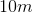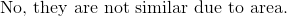ACT Math : Other Quadrilaterals
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : How To Find If Quadrilaterals Are Similar
The sides of rectangle A measure to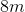 
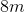
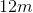
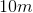
In similar rectangles, the ratio of the sides must be equal.
To solve this question, the following equation must be set up:
We then must cross multiply, which leaves us with:
Lastly, we divide both sides by 8 to solve for the missing side:
Therefore, the longer sides of the rectangle are each 
Example Question #181 : Quadrilaterals
Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?
Set up the proportion to determine if the ratios of both rectangles are equal.
If they are, then they are similar.
These are not similar rectangles since their ratios are not the same.
Example Question #181 : Quadrilaterals
A square has a length of 
A square with a length of 
Example Question #414 : Act Math
If the rectangle has side lengths of 
Use the Pythagorean Theorem to solve for the diagonal.
Example Question #3 : How To Find The Length Of The Diagonal Of A Quadrilateral
In the parallelogram above, 
In a parallelogram, the two diagonals bisect each other at their centers. Therefore, 
Plugging this value back into both equations, then adding those values together, gives us our answer of 
Example Question #1 : How To Find The Area Of A Quadrilateral
Jane plans to re-tile her kitchen with tiles that have a length of 
When attempting to solve how many pieces of a particular object you need to cover a certain area, always make sure that your units of measurement (for the object and for the area you are covering) are the same. In the case of this question, the units of measurement are different, so you must first convert all measurements to use the same unit.
Since the tiles being used to cover the area are measured in inches, convert all units given to inches:
Length: 
Width: 
Then, find the area of the entire space you are covering. Since the space is rectangular (this can be assumed since only length and width are given as measurements), multiply the length and width to find the total area: 
Next, find the area of each of the tiles: 
The answer is 
Example Question #1 : How To Find The Area Of A Quadrilateral
Vikram is looking at a scale drawing of a room he is building. The drawing is of a rectangle that measures 
When solving such problems, always make sure that your units of measurement are all the same. In the case of this problem, you must convert feet to inches. Multiply 30 by 12 in order to get its equivalent in inches.
We know that the 30 feet corresponds with the side of the drawing that is 18 inches because it is stated that the longest side will be 30 feet. Divide 360 by 18 in order to find the ratio of the actual size of the room to the measurements on the drawing
This means that the actual measurements of the room are 20 times the measurements of the drawing. Multiply 20 times 12 in order to find the measurement of the shorter side in inches.
Divide both the 360 and 240 by 12 to convert the measurements back into feet.
Then multiply the results to get the final answer.
Example Question #1 : How To Find The Area Of A Quadrilateral
If a trapezoid has base lengths of 
Use the formula for area of a trapezoid:
Where 
In this case:
Example Question #1 : How To Find The Area Of A Quadrilateral
A parallelogram has a side length of 
Use the formula for area of a parallelogram:
Where 
In this case:
Example Question #1 : How To Find The Length Of The Side Of A Quadrilateral
Find the length of a rectangle if the area is 
Write the formula to solve the area of a rectangle.
Substitute the dimension and area to solve for the length.
All ACT Math Resources
