ACT Math : How to find the diagonal of a cube
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Diagonal Of A Cube
Find the length of the diagonal of a cube with side length of 
We begin with a picture, noting that the diagonal, labeled as 
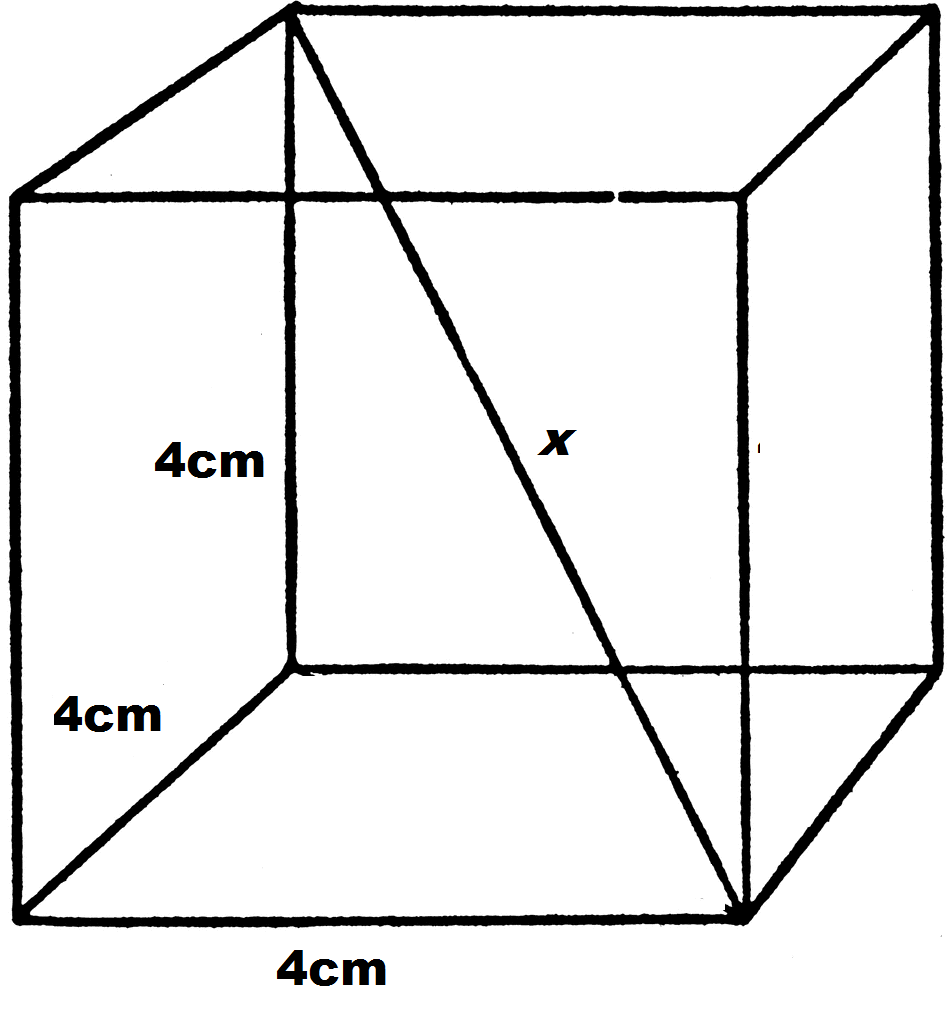
However, the trick to solving the problem is to also draw in the diagonal of the bottom face of the cube, which we labeled 
Note that this creates two right triangles. Though our end goal is to find 
Now that we know the value of 
Taking the square root of both sides and simplifying gives the answer.
Example Question #1 : How To Find The Diagonal Of A Cube
What is the diagonal length for a cube with volume of 
Recall that the volume of a cube is computed using the equation
So, for our data, we know:
Using your calculator, take the cube root of both sides. You can always do this by raising 
If you get 
This is 
Example Question #3 : How To Find The Diagonal Of A Cube
What is the length of the diagonal of a cube with a volume of 
Recall that the diagonal of a cube is most easily found when you know that cube's dimensions. For the volume of a cube, the pertinent equation is:
Now, you could factor this by hand or use your calculator. You will see that 
Now, we find the diagonal by using a three-dimensional version of the Pythagorean Theorem / distance formula:
You can rewrite this:
Certified Tutor
Certified Tutor
All ACT Math Resources
