All ACT Math Resources
Example Questions
Example Question #1 : How To Evaluate A Fraction
Evaluate the following equation when 
1. Plug in 

2. Perform the above operations.
Example Question #2 : How To Evaluate A Fraction
Mary walked to school at an average speed of 2 miles per hour and jogged back along the same route at an average speed of 6 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the round trip?
Since Mary traveled 3 times as quickly coming from school as she did going to school (6 miles per hour compared to 2 miles per hour), we know that Mary spent only a third of the time coming from school as she did going. If x represents the number of hours it took to get to school, then x/3 represents the number of hours it took her to return.
Knowing that the total trip took 1 hour, we have:
x + x/3 = 1
3x/3 + 1x/3 = 1
4x/3 = 1
x = 3/4
So we know it took Mary 3/4 of an hour to travel to school (and the remaining 1/4 of an hour to get back).
Remembering that distance = rate * time, the distance Mary traveled on her way to school was (2 miles per hour) * (3/4 of an hour) = 3/2 miles. Furthermore, since she took the same route coming back, she must have traveled 3/2 of a mile to return as well.
Therefore, the the total number of miles in Mary's round trip is 3/2 miles + 3/2 miles = 6/2 miles = 3 miles.
Example Question #3 : How To Evaluate A Fraction
If 

To raise 


Example Question #4 : How To Evaluate A Fraction
Solve ![]()
0
no solution
infinitely many solutions
–1
infinitely many solutions
The common denominator of the left side is x(x–1). Multiplying the top and bottom of 1/x by (x–1) yields
![]()
![]()
![]()
![]()
Since this statement is true, there are infinitely many solutions.
Example Question #5 : How To Evaluate A Fraction
For this question, the following trigonometric identities apply:

Simplify:
To begin a problem like this, you must first convert everything to 

Since 

From here we combine the numerator and denominators of each fraction together to easily see what we can combine and cancel.
Since there is a 

Example Question #6 : How To Evaluate A Fraction
If 3x = 12, y/4 = 10, and 4z = 9, what is the value of (10xyz)/xy?
22 1/2
360
160
4 1/2
10
22 1/2
Solve for the variables, the plug into formula.
x = 12/3 = 4
y = 10 * 4 = 40
z= 9/4 = 2 1/4
10xyz = 3600
Xy = 160
3600/160 = 22 1/2
Example Question #7 : How To Evaluate A Fraction
If 



In order to solve 




Then:
Finally:
With the values of 


Example Question #6 : How To Evaluate A Fraction
If 


In order to solve 


Find the Least Common Multiple (LCM) of the fractional terms in the denominator and find the equivalent fractions with the same common denominator:
Finally, in order to divide by a fraction, we must multiply by the reciprocal of the fraction:
Example Question #7 : How To Evaluate A Fraction
Find the value of 


In order to solve for 


Then, find the Least Common Multiple (LCM) of the two fractions and generate equivalent fractions with the same denominator:
Finally, simplify the equation:
Example Question #8 : How To Evaluate A Fraction
Factor out 7 from the numerator:
This simplifies to 7.
Certified Tutor
Certified Tutor
All ACT Math Resources




















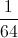

![w^\frac{2}{3}=\sqrt[3]{w^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177545/gif.latex)
![(\frac{1}{8})^\frac{2}{3}=\sqrt[3]{(\frac{1}{8})^2}=\sqrt[3]{\frac{1}{64}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177546/gif.latex)
![\sqrt[3]{\frac{1}{64}}=\frac{1}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177547/gif.latex)



























































