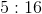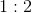For this problem, we need to find the number of employees who fall into the categories described, keeping in mind that multiple portions of the pie chart must be accommodated for. Then, we can fit them into a ratio:

For the "2 to 9 years" portion of the financial industry, include

(0.2 + 0.18)(12,000,000) = 4,560,000 workers.

For the "0 to 4 years" portion of the construction industry, include

(0.15 + 0.2)(8,000,000) = 2,800,000 workers.

Now divide and simplify to find the ratio:

4,560,000/2,800,000 = 8/5.

Since the ratios are fixed, regardless of the actual values of , , or , we can let  and

In order to convert to a form where we can relate  to , we must set the coefficient of  of each ratio equal such that the ratio can be transferred. This is done most easily by finding a common multiple of  and  (the ratio of  to  and , respectively) which is

Thus, we now have  and .

Setting the  values equal, we get , or a ratio of 

First, begin by calculating the total number of each item that there will be at the end of the process.

Cups: 

Saucers: 

The ratio of cups to saucers will thus be:

In order to solve this problem, create an equation that summarizes the roof repair cost for each company. Begin by composing a formula for Company A, which charges 120 dollars upfront and 15 dollars per hour of labor.

Now, Company B charges 95 dollars upfront and 20 dollars per hour of labor. We can write the following equation:

The question asks us to find how many hours of labor that a repair must take in order for Company A to be cheaper than Company B. In other words, we need to compose an inequality in which the cost of Company A is less than the cost of Company B. We will substitute the variable  for hours and solve. 

Subtract  from each side of the inequality.

Subtract 95 from both sides of the inequality.

Divide both sides of the inequality by 5. 

If the repair will take more than 5 hours, Company A will be cheaper.

First, let's assign variables to the names of the individuals to represent their age in 2013. 

In 2013, Molly was three times older than Steve; therefore, we can write the following expression:

We are also told that in 2016, Molly will be two times older than Steve; thus, we can write another expression: 

.

We can then substitute  in for  in the second equation to arrive at the following:

Using the given information we can generate the following two proportions:

 and

Next, cross-multiply each proportion to come up with the following two equations: 

 and  

Each equation shares a term with the  variable. We need to make this variable equal in both equations to continue. Multiply the first equation by a factor of 3 and the second by a factor of 2, so that the  terms are equivalent. Let's start with the first equation.

Now, we will perform a similar operation on the second equation.

Now, we can set these equations equal to one another.

Drop the equivalent  terms.

 The proportion then becomes the following: 

 or 

Assign a variable to science books since everything in the question can be written in terms of science books.

Write an expression for the phrase "twice as many comic books as science books."

To create an equation for the cost of the books, we can write the following:

Substitute in the known values and variables.

Jeff purchased 2 science books and 4 comic books.

In general for work problems:  W₁ + W₂ = 1 where Work = Rate x Time

Note, 1 represents the completed job assignment.

For example, W₁ is the rate that the first person would finish the job multiplied by the time it would take two or more people to finish the job completely.

1/3x + 1/2x = 1 where x is the time it would take for both people to complete the job.

Find a common denominator to add the fractions, then solve for x.

x = 1.2 days for one house, but the questions asks about two houses, so the correct answer is 2.4 days.

Property area = 10,000 ft x 40,000 ft = 400,000,000 ft²

Acreage = 400,000,000 ft² / 43,560 ft² per acre = 9,183 acres

Taxes = $3.50 per acre x 9,183 acres = $32,140

Remember that distance = rate x time

For the first route, we can set up an equation where the total distance (36 + 44) equals the rate (65 mph) multiplied by the time:

36 +44 = 65t

80 = 65t

t = 80/65 = 1.23 hrs = 1 hr, 14 min

To find the time taken for the second route, we first figure out the distance traveled by using the Pythagorean Theorem.

We know that the "legs" of the right triangle are 44 and 36, where the hypotenuse is the straightline distance (northwest), directly to the destination:

a²+b²=c²                                                                                                       

44²+36²=c²                                                                              

3232=c²                                                                                     

c=56.85

56.85=40t

56.85/40=t

t=1.42 hrs=1 hr, 25 min                                                         

1 hr. 25 min. – 1 hr. 14 min. = 11 min.