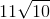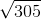All ACT Math Resources
Example Questions
Example Question #51 : Basic Squaring / Square Roots
Simplify:
Again here, if no perfect square is easily recognized try dividing by 


Note that the 


Example Question #261 : New Sat Math Calculator
Simplify:
To solve, simply find a perfect square factor and pull it out of the square root.
Recall the factors of 48 include (16, 3). Also recall that 16 is a perfect square since 4*4=16.
Thus,
Example Question #53 : Basic Squaring / Square Roots
Solve:
The trick to these problems is to simplify the radical by using the following rule: 


Example Question #1 : How To Find The Common Factors Of Squares
Simplify:
When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.
What are the factors of 24,300?
24,300 can be factored into:
When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is 
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267786/gif.latex)
But 243 can also be factored:
Following the same principle as for the 100, the problem would become![9\cdot 10\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267789/gif.latex)
9 and 10 may be multiplied together, yielding the final simplified answer of
Example Question #1 : How To Find The Common Factors Of Squares
To solve the equation 
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
Example Question #61 : Basic Squaring / Square Roots
If (x - 3)2 = 64, what is a possible value of x?
In order to solve for x, we must first take the square root of both sides.
(x - 3)2 = 64
(x - 3) = +/- 8
The square root of 64 is either 8 or -8. We then solve the equation with both possible values of the square root of 64.
x - 3 = 8 (Add 3 to both sides.)
x = 11
x - 3 = -8 (Add 3 to both sides.)
x = -5
x = 11 or -5. -5 is the only possible value of x that is an answer choice.
Example Question #81 : Arithmetic
Solve: 3³
99
9
93
18
27
27
When using a cube root. 3³ becomes 3 * 3 * 3.
3 * 3 = 9
9 * 3 = 27
Example Question #1 : Other Squaring / Square Roots
When you square the following numbers, which one results in an irrational number?
A rational number is any number than can be expressed as a fraction or a quotient of two integers. The square of π is still an irrational number. (√(2))2 = 2, (1/3)2 = 1/9, (7/17)2 = 49/289, (1/2)2 = 1/4, all can be writen in fractional form, and are thus, rational numbers.
Example Question #61 : Basic Squaring / Square Roots
How much larger is the sum of the squares of –2, –3, and 4 than the sum of these integers?
–1
25
Infinitely larger
30
17
30
The square of –2 is 4, of –3 is 9, and of 4 is 16.
The sum of these squares is 29.
The sum of (–2) + (–3) + (4) is –1.
29 – (–1) = 30
Example Question #61 : Basic Squaring / Square Roots
is between what two integers?









Therefore, 


Certified Tutor
Certified Tutor
All ACT Math Resources





















![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267782/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267774/gif.latex)
![900\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267780/gif.latex)
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267778/gif.latex)
![9\sqrt[2]{300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267781/gif.latex)
![90\sqrt[2]{270}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267776/gif.latex)
![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267783/gif.latex)
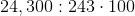


![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267790/gif.latex)