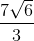It might be a little difficult taking a fourth root of 100 to isolate x by itself; it might be easier to select an integer and take that number to the fourth power. For example 3⁴ = 81 and 4⁴ = 256. Since 3⁴ is less than 100 and 4⁴ is greater than 100, x would lie between 3 and 4.

The ratio of two numbers is merely the division of the two values. Therefore, for the information given, we know that the ratio of 

 to 

can be rewritten:

Now, we know that the square root in the denominator can be "distributed" to the numerator and denominator of that fraction:

Thus, we have:

To divide fractions, you multiply by the reciprocal:

Now, since there is one  in , you can rewrite the numerator:

This gives you:

Rationalize the denominator by multiplying both numerator and denominator by :

Let's be careful how we write the numerator so as to make explicit the shared factors:

Now, reduce:

This is the same as 

To find a ratio like this, you need to divide  by . Recall that when you have the square root of a fraction, you can "distribute" the square root to the numerator and the denominator. This lets you rewrite  as:

Next, you can write the ratio of the two variables as:

Now, when you divide by a fraction, you can rewrite it as the multiplication by the reciprocal. This gives you:

Simplifying, you get:

You should rationalize the denominator:

This is the same as:

Find the Sum:

Simplify the radicals:

The first step when adding square roots is to simplify each term as much as possible. Since the first term has a square within the square root, we can reduce to . Now each term has only prime numbers within the sqaure roots, so nothing can be further simplified and our new expression is .

Only terms that have the same expression within the sqaure root can be combined. In this question, these are the first and third terms. When combining terms, the expression within the square root stays the say, while the terms out front are added. Therefore we get . Since the second term of the original equation cannot be combined with any other term, we get the final answer of .

Take each fraction separately first:

(2√3)/(√2) = [(2√3)/(√2)] * [(√2)/(√2)] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6

Similarly:

(4√2)/(√3) = [(4√2)/(√3)] * [(√3)/(√3)] = (4√6)/3 = (4/3)√6

Now, add them together:

√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6

Begin by factoring out each of the radicals:

For the first two radicals, you can factor out a  or :

The other root values cannot be simply broken down. Now, combine the factors with :

This is your simplest form.

Begin by getting your  terms onto the left side of the equation and your numeric values onto the right side of the equation:

Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:

Now, square both sides:

Solve by dividing both sides by :

Begin simplifying by breaking apart the square roots in question. Thus, you know:

Now, with square roots, you can combine factors just as if a given root were a variable. So, just as , so too does .

Begin simplifying by breaking apart the square roots in question. Thus, you know:

Now, with square roots, you can combine factors just as if a given root were a variable. So, just as , so too does .