Graphically, the y-intercept is the point at which the graph touches the y-axis.  Algebraically, it is the value of  when .

Here, we are given the function .  In order to calculate the y-intercept, set  equal to zero and solve for .

So the y-intercept is at .

Graphically, the x-intercept is the point at which the graph touches the x-axis.  Algebraically, it is the value of  for which .

Here, we are given the function .  In order to calculate the x-intercept, set  equal to zero and solve for .

So the x-intercept is at .

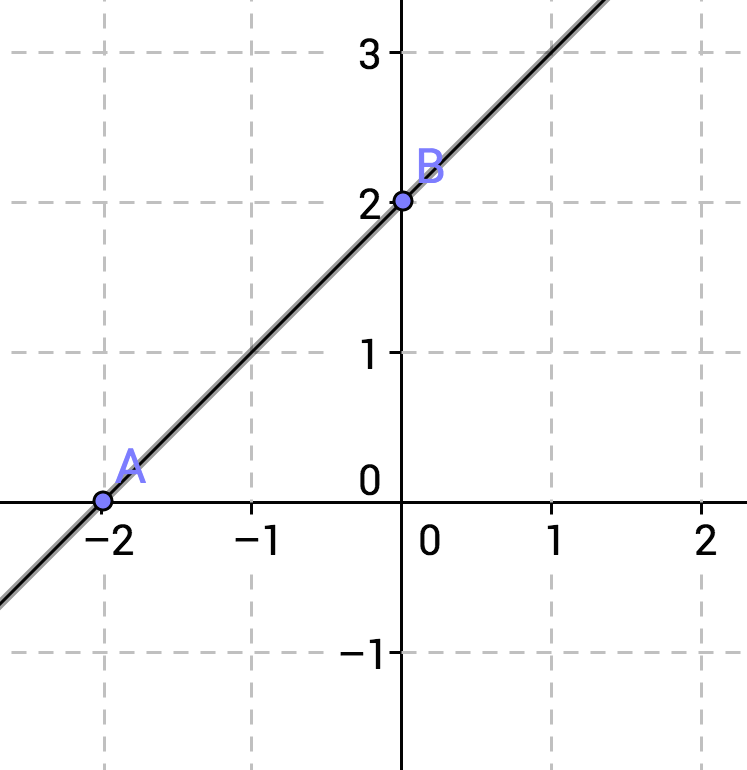
A line is defined by any two points on the line.  It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.

Let .  Then

So our first set of points (which is also the y-intercept) is 

Let .  Then

So our second set of points (which is also the x-intercept) is .

There are four shifts of the graph y = f(x):

y = f(x) + c shifts the graph c units upwards.

y = f(x) – c shifts the graph c units downwards.

y = f(x + c) shifts the graph c units to the left.

y = f(x – c) shifts the graph c units to the right.

This question relies on both the vertical-line test and the definition of a function. We need to use the vertical-line test to determine which of the graphs is not a function (i.e. the graph that has more than one output for a given input). The vertical-line test states that a graph represents a function when a vertical line can be drawn at every point in the graph and only intersect it at one point; thus, if a vertical line is drawn in a graph and it intersects that graph at more than one point, then the graph is not a function. The circle is the only answer choice that fails the vertical-line test, and so it is not a function.

For the ordered pair 

The first number is for the x-axis, so because it is positive you go right .

The second number is for the y-axis, so because it is positive you go up .

For the ordered pair  we would do the following.

The first number is for the x-axis, so because it is negative you go left  units.

The second number is for the y-axis, so because it is positive you go up  units.

To find out which quadrant a point lives in, we need to remember the qualities of each quadrant. By qualities, I mean the signs associated with the x and y values which are dependent on the quadrant the point resides in.

All coordinate pairs that are in Quadrant I will have a positive x value and a positive y value.

All coordinate pairs that are in Quadrant II will have a negative x value and a positive y value.

All coordinate pairs that are in Quadrant III will have a negative x value and a negative y value.

All coordinate pairs that are in Quadrant IV will have a positive x value and a negative y value.

For the point  we see that both the x and y values are negative therefore, the point lies in the third quadrant. We can also check this by starting from the origin and going left 3 units and down 3 units. This will end up in the lower-left section of the coordinate-plane, which is Quadrant III.

Find the x-coordinate by going right on the horizontal x-axis until you come across the line that is directly under the point. The x-coordinate is .

Now, continue up until you reach the point and look across to the vertical y-axis. The y-coordinate is .

 is then the coordinate of the point.

Find the x-coordinate by going right on the horizontal x-axis until you come across the line that is directly under the point. The x-coordinate is .

Now, continue up until you reach the point and look across to the vertical y-axis. The y-coordinate is .

 are the coordinates for point A.