To FOIL this binomial distribution, we simply distribute the terms in a specific order:

Multiply the First terms:

Multiply the Outer terms:

Multiply the Inner terms:

Multiply the Last terms:

Lastly, combine any terms that allow this (usually, but not always, the two middle terms):

Arrange your answer in descending exponential form, and you're done.

To FOIL this binomial distribution, we simply distribute the terms in a specific order:

Multiply the First terms:

Multiply the Outer terms:

Multiply the Inner terms:

Multiply the Last terms:

Lastly, combine any terms that allow this (usually, but not always, the two middle terms):

Arrange your answer in descending exponential form, and you're done.

The trick to this expression is to remember that only those terms which share both common variables AND common exponents are additive. In other words, you cannot add  any more than you can add .

To FOIL this binomial distribution, we simply distribute the terms in a specific order:

Multiply the First terms:

Multiply the Outer terms:

Multiply the Inner terms:

Multiply the Last terms:

Lastly, combine any terms that allow this (usually, but not always, the two middle terms). In this case, no two terms are compatible.

Arrange your answer in descending exponential form, and you're done.

Use the grid method to FOIL.

Combine the like terms.

Using FOIL which stands for the multiplication process between the Firsts, Outers, Inners, and Lasts, we end up with the expression 

.

From there, combine the like terms  to get .

Therefore the product becomes,

This question is asking you to multiply two binomials. You can use the grid method for FOIL.

Using our properties of exponents, we could rewrite  as  

This means that when we input , we first subtract 2, then take this to the fourth power, then take the fifth root, and then add three. We want to look at these steps individually and see whether there are any values that wouldn’t work at each step. In other words, we want to know which  values we can put into our function at each step without encountering any problems.

The first step is to subtract 2 from . The second step is to take that result and raise it  to the fourth power. We can subtract two from any number, and we can take any number to the fourth power, which means that these steps don't put any restrictions on .

Then we must take the fifth root of a value. The trick to this problem is recognizing that we can take the fifth root of any number, positive or negative, because the function  is defined for any value of ; thus the fact that  has a fifth root in it doesn't put any restrictions on , because we can add three to any number; therefore, the domain for  is all real values of .

The domain of the function is all real numbers except x = –3. When x = –3, f(–3) is undefined.

When x = 0 or x = 3, the function is undefined due to its denominator. 

Thus the domain is all real numbers x, such that x is not equal to 0 or 3.

If a value of x makes the denominator of a equation zero, that value is not part of the domain. This is true, even here where the denominator can be "cancelled" by factoring the numerator into

and then cancelling the 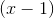 from the numerator and the denominator. 

This new expression,  is the equation of the function, but it will have a hole at the point where the denominator originally would have been zero. Thus, this graph will look like the line  with a hole where , which is 

.

Thus the domain of the function is all  values such that