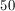Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : ACT Math

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find Negative Cosine

What is the cosine of the angle formed between the origin and the point (-6,-11) if that angle is formed with one side of the angle beginning on the -axis and then rotating counter-clockwise to ? Round to the nearest hundredth.

Possible Answers:

0.48

0.78

-0.48

0.88

-0.88

Correct answer:

-0.48

Explanation:

Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the -axis as your reference point for your angle. (Hence, it is called the "reference angle.")

Now, it is easiest to think of this like you are drawing a little triangle in the third quadrant of the Cartesian plane. It would look like:

Cos611

So, you first need to calculate the hypotenuse. You can do this by using the Pythagorean Theorem, a^2+b^2=c^2 , where and are the lengths of the legs of the triangle and the length of the hypotenuse. Rearranging the equation to solve for , you get:

$c=\sqrt{a^2+b^2}$

Substituting in the given values:

$c=\sqrt{6^2+11^2}=\sqrt{36+121}=\sqrt{157}$

So, the cosine of an angle is:

$\frac{adjacent}{hypotenuse}$ or, for your data, $\frac{6}{\sqrt{157}}$ .

This is approximately 0.47885213068056 . Rounding, this is 0.48 . However, since (-6,-11) is in the third quadrant your value must be negative: -0.48 .

Report an Error

Example Question #3 : How To Find Negative Cosine

What is the cosine of the angle formed between the origin and the point (-3,7) if that angle is formed with one side of the angle beginning on the -axis and then rotating counter-clockwise to (-3,7) ? Round to the nearest hundredth.

Possible Answers:

0.40

-0.61

-0.40

-0.94

0.94

Correct answer:

-0.40

Explanation:

Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the -axis as your reference point for your angle. (Hence, it is called the "reference angle.") Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

Cos37

So, you first need to calculate the hypotenuse:

$h=\sqrt{3^2+7^2}=\sqrt{9+49}=\sqrt{56}$

So, the cosine of an angle is:

$\frac{adjacent}{hypotenuse}$ or, for your data, $\frac{3}{\sqrt{56}}$ .

This is approximately 0.40089186286863 . Rounding, this is 0.40 . However, since (-3,7) is in the second quadrant your value must be negative: -0.40 .

Report an Error

Example Question #2 : How To Find Negative Cosine

To the nearest , what is the cosine of the angle formed between the origin and (-4, -14) ? Assume a counterclockwise rotation.

Possible Answers:

-.275

-.332

-.605

-.545

-.554

Correct answer:

-.275

Explanation:

If the point to be reached is (-4, -14) , then we may envision a right triangle with sides and , and hypotenuse . The Pythagorean Theorem tells us that a^2 + b^2 = c^2 , so we plug in and find that: 4^2 + 14^2 = c^2 = 212

Thus, $c = \sqrt{212} = 2\sqrt{53}$

Now, SOHCAHTOA tells us that $\textup{cosine}= \frac{\textup{adjacent}}{\textup{hypotenuse}}$ , so we know that:

$cos x^{\circ} = \frac{4}{2\sqrt{53}} \approx 0.2747$

Thus, our cosine is approximately . However, as we are in the third quadrant, cosine must be negative! Therefore, our true cosine is -.275 .

Report an Error

Example Question #3 : How To Find Negative Cosine

On a grid, what is the cosine of the angle formed between a line from the origin to (-3, 9) and the x-axis?

Possible Answers:

$-\frac{\sqrt{10}}{10}$

$-\frac{3\sqrt{10}}{10}$

$\frac{3\sqrt{10}}{10}$

$\textup{None of the answers provided is correct.}$

$\frac{\sqrt{10}}{10}$

Correct answer:

$-\frac{\sqrt{10}}{10}$

Explanation:

If the point to be reached is (-3, 9) , then we may envision a right triangle with sides and , and hypotenuse . The Pythagorean Theorem tells us that a^2 + b^2 = c^2 , so we plug in and find that: 3^2 + 9^2 = c^2 = 90 .

Thus, $c = \sqrt{90} = 3\sqrt{10}$ .

Now, SOHCAHTOA tells us that $\textup{cosine} = \frac{\textup{adjacent}}{\textup{hypotenuse}}$ , so we know that:

$\textup{cos} x^{\circ} = \frac{3}{3\sqrt{10}} = \frac{1}{\sqrt{10}} = \frac{\sqrt{10}}{10}$

Thus, our cosine is approximately $\frac{\sqrt{10}}{10}$ . However, as we are in the second quadrant, cosine must be negative! Therefore, our true cosine is $-\frac{\sqrt{10}}{10}$ .

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Solve for .

$\frac{16}{x + 7} = \frac{2}{6}$

Possible Answers:

Correct answer:

Explanation:

Cross multiply. 96 = 2 (x+7)

Dsitribute. 96 = 2x + 14

Solve for . 96 - 14 = 2x

82 = 2x

41 = x

Report an Error

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

The quotient of a fraction is 12x . If the numerator is 48x^3 , what is the value of the denominator?

Possible Answers:

.25x

6x^3

4x^2

576x^4

8x^2

Correct answer:

4x^2

Explanation:

Step 1: Set up the equation

$\frac{48x^3}{D}=12x$

Step 2: Solve for D

$\frac{48x^3}{D}=12x \rightarrow 48x^3= 12x \cdot D\rightarrow \frac{48x^3}{12x}=D$

D = 4x^2

Report an Error

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Solve for :

$\frac{x+1}{4}-\frac{x}{3}=6$

Possible Answers:

x=-69

x=26

x=42

x=-72

x=60

Correct answer:

x=-69

Explanation:

Solve for x:

$\frac{x+1}{4}-\frac{x}{3}=6$

Step 1: Find the least common denominator, , and adjust the fractions accordingly:

$\left (\frac{3}{3} \right )\cdot \left ( \frac{x+1}{4} \right ) - \left ( \frac{4}{4} \right )\cdot \left ( \frac{x}{3} \right )=6$

$\left ( \frac{3x+3}{12} \right )-\left ( \frac{4x}{12} \right )=6$

Solve for :

$\frac{3x+3-4x}{12}=6$

3x+3-4x=72

-x=69

x=-69

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

If $\frac{6}{x}=\frac{9}{19}$ , then what is the value of ?

Possible Answers:

none of these

38/3

3/38

7/12

9/114

Correct answer:

38/3

Explanation:

cross multiply:

(6)(19) = 9x

114=9x

x = 38/3

Report an Error

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

$\dpi{100} \small \frac{4 }{x} = \frac{2}{25}$

Find x.

Possible Answers:

None

$\dpi{100} \small 0.25$

$\dpi{100} \small \frac{8}{25}$

$\dpi{100} \small \frac{25}{8}$

$\dpi{100} \small 50$

Correct answer:

$\dpi{100} \small 50$

Explanation:

Cross multiply:

$\dpi{100} \small 4 \times 25 = 2x$

$\dpi{100} \small 100 = 2x$

$\dpi{100} \small x = 50$

Report an Error

Example Question #3 : How To Solve For A Variable As Part Of A Fraction

The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.

Possible Answers:

$\frac{1}{2}$

$\frac{1}{3}$

Correct answer:

Explanation:

Let numerator = N and denominator = D.

According to the first statement,

N = (D x 5) + 4.

According to the second statement, N / 2 = 3 * D.

Let's multiply the second equation by –2 and add itthe first equation:

–N = –6D

+[N = (D x 5) + 4]

–6D + (D x 5) + 4 = 0

–1D + 4 = 0

D = 4

Thus, N = 24.

Therefore, N/D = 24/4 = 6.

Report an Error

View ACT Math Tutors

Ana
Certified Tutor

Grand Canyon University, Bachelors, Education. Grand Canyon University, Masters, Education.

View ACT Math Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

View ACT Math Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Atlanta, MCAT Courses & Classes in San Diego, MCAT Courses & Classes in Atlanta, SAT Courses & Classes in San Diego, SSAT Courses & Classes in Houston, SAT Courses & Classes in New York City, LSAT Courses & Classes in Atlanta, MCAT Courses & Classes in Denver, GMAT Courses & Classes in San Diego

Popular Test Prep

GRE Test Prep in San Diego, SAT Test Prep in Atlanta, SAT Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Miami, SSAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Atlanta, LSAT Test Prep in Chicago, SAT Test Prep in Houston, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : ACT Math

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : How To Find Negative Cosine

Example Question #3 : How To Find Negative Cosine

Example Question #2 : How To Find Negative Cosine

Example Question #3 : How To Find Negative Cosine

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Example Question #3 : How To Solve For A Variable As Part Of A Fraction

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: