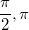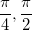We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Trigonometry : Unit Circle and Radians

Study concepts, example questions & explanations for Trigonometry

Create An Account

All Trigonometry Resources

6 Diagnostic Tests 155 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Unit Circle And Radians

Convert $\frac{11\pi}{5}$ into degrees.

Possible Answers:

$300\degree$

$400\degree$

$395\degree$

$396\degree$

Correct answer:

$396\degree$

Explanation:

To convert from radians to degrees, you must multiply the angle by $\frac{180\degree}{\pi}$ to cancel the $\pi$ units.

This will get you

$11\cdot \frac{180\degree}{5}=396^\circ$

Report an Error

Example Question #62 : Unit Circle And Radians

Convert $\frac{2\pi}{5}$ to degrees:

Possible Answers:

$114^{\circ}$

$\frac{2}{5}^{\circ}$

$72\pi$

$72^{\circ}$

$36^{\circ}$

Correct answer:

$72^{\circ}$

Explanation:

To convert radians to degrees, we need to multiply the given radians by $\frac{180^{\circ}}{\pi}$ .

$\frac{2\pi}{5}*\frac{180^{\circ}}{\pi}=\frac{360^{\circ}}{5}=72^{\circ}$

Report an Error

Example Question #44 : Circles

Give your answer in terms of $\pi$ .

Convert $165^{\circ}$ to radians:

Possible Answers:

$\frac{11\pi}{12}$

$\frac{12\pi}{11}$

$\frac{\pi}{12}$

$\frac{11\pi}{24}$

$\frac{11\pi}{6}$

Correct answer:

$\frac{11\pi}{12}$

Explanation:

To convert degrees to radians, we need to multiply the given degree by $\frac{\pi}{180^{\circ}}$ .

$165*^{\circ}\frac{\pi}{180^{\circ}}=\frac{165\pi}{180}$

To simplify, we get:

$\frac{11\pi}{12}$

Report an Error

Example Question #63 : Unit Circle And Radians

Convert $52^{\circ}$ to radians.

Possible Answers:

$\frac{\pi}{2}$

$\frac{\pi}{5}$

$\tfrac{17}{12}\pi$

$\tfrac{13}{45}\pi$

$\frac{2\pi}{3}$

Correct answer:

$\tfrac{13}{45}\pi$

Explanation:

To convert between degrees and radians, multiply by $\frac{\pi }{180^{\circ}}$ or $\frac{180^{\circ}}{\pi}$ .

Since we start in degrees, we use $\frac{\pi }{180^{\circ}}$ :

$\frac{52^{\circ}}{1}\times\frac{\pi}{180^{\circ}}=\frac{52}{180}\pi$

which simplifies to $\tfrac{13}{45}\pi$ .

Report an Error

Example Question #24 : Radians

Convert $\frac{7\pi}{4}$ radians into degrees.

Possible Answers:

$285^{\circ}$

$345^{\circ}$

$270^{\circ}$

$225^{\circ}$

$315^{\circ}$

Correct answer:

$315^{\circ}$

Explanation:

Recall the definition of "radians" derived from the unit circle:

$180^{\circ} = \pi rad$

The quantity of radians given in the problem is $\frac{7\pi}{4}$ . All that is required to convert this measure into degrees is to denote the unknown angle measure in degrees by $\Theta$ and set up a proportion equation using the aforementioned definition relating radians to degrees:

$\frac{180^{\circ}}{\Theta} = \frac{\pi rad}{\frac{7\pi}{4} rad}$

Cross-multiply the denominators in these fractions to obtain:

$1260^{\circ}\pi rad=4\Theta\pi rad$

$315^{\circ}\pi rad =\Theta\pi rad$ .

Canceling like terms in these equations yields

$\Theta = 315^{\circ}$

Hence, the correct angle measure of $\frac{7\pi}{4}$ in degrees is $315^{\circ}$ .

Report an Error

Example Question #63 : Unit Circle And Radians

What are the ways to write 360^o and 720^o in radians?

Possible Answers:

$\small \frac{\pi}{4},\frac{\pi}{2}$

$\small 2\pi,4\pi$

$\small \pi,2\pi$

$\small \small 0,\pi$

$\small \frac{\pi}{2},\pi$

Correct answer:

$\small 2\pi,4\pi$

Explanation:

$\small 360^o=2\pi$ on the unit circle.

$\small \small \small 720^o=4\pi$ on the unit circle.

Report an Error

Example Question #64 : Unit Circle And Radians

Which of the following is not an angle in the unit circle?

Possible Answers:

$\frac{\pi}{5}$

$\frac{5\pi}{6}$

$\frac{3\pi}{4}$

$\frac{2\pi}{3}$

$\pi$

Correct answer:

$\frac{\pi}{5}$

Explanation:

The unit circle is in two increments: $\frac{\pi}{6}$ : $(\frac{\pi}{6},\frac{2\pi}{6},\frac{3\pi}{6})$ , etc. and $\frac{\pi}{4}$ : $(\frac{\pi}{4},\frac{2\pi}{4},\frac{3\pi}{4})$ , etc. The only answer choice that is not a multiple of either $\frac{\pi}{6}$ or $\frac{\pi}{4}$ is $\frac{\pi}{5}$ .

Report an Error

Example Question #443 : Trigonometry

What is the equivalent of $72^{\circ}$ , in radians?

Possible Answers:

$\frac{\pi }{10}$

$\frac{2\pi }{5}$

$\frac{2\pi}{10}$

$\frac{\pi }{5}$

$\pi$

Correct answer:

$\frac{2\pi }{5}$

Explanation:

To convert from degrees to radians, use the equality

$2\pi = 360^{\circ}$ or $\pi = 180^{\circ}$ .

From here we use $\frac{\pi}{180^{\circ}}$ as a unit multiplier to convert our degrees into radians.

$\left (72^{\circ} \right )\left ( \frac{\pi }{180^{\circ}} \right ) = \frac{2\pi}{5}$

Report an Error

Example Question #4 : Angles In The Unit Circle

What is the value of tan(45) ?

Possible Answers:

$\frac{\sqrt{3}}{2}$

$\frac{\sqrt{2}}{2}$

$\frac{1}{2}$

Correct answer:

Explanation:

To help with this one, draw a 45-45-90 triangle. With legs equal to 1 and a hypotenuse of $\sqrt2$ .

Then, use the definition of tangent as opposite over adjacent to find the value.

Since the legs are congruent, we get that the ratio is 1.

Report an Error

Example Question #5 : Angles In The Unit Circle

What is sin(90) ?

Possible Answers:

$\frac{1}{2}$

$\frac{\sqrt{3}}{2}$

Correct answer:

Explanation:

Recall that on the unit circle, sine represents the y coordinate of the unit circle.

Then, since we are at 90˚, we are at the positive y axis, the point (0,1).

At this point on the unit circle, the y value is 1.

Thus sin(90)=1 .

Report an Error

View Trigonometry Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View Trigonometry Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View Trigonometry Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

All Trigonometry Resources

6 Diagnostic Tests 155 Practice Tests Question of the Day Flashcards Learn by Concept

Trigonometry Tutors in Top Cities:

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Atlanta, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Phoenix, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in Washington DC, SAT Courses & Classes in New York City, ISEE Courses & Classes in New York City, Spanish Courses & Classes in New York City, LSAT Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in Boston, SAT Test Prep in Seattle, GMAT Test Prep in Atlanta, GMAT Test Prep in Washington DC, ISEE Test Prep in New York City, LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Philadelphia, LSAT Test Prep in Atlanta, LSAT Test Prep in Miami, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Trigonometry : Unit Circle and Radians

Study concepts, example questions & explanations for Trigonometry

All Trigonometry Resources

Example Questions

Example Question #61 : Unit Circle And Radians

Example Question #62 : Unit Circle And Radians

Example Question #44 : Circles

Example Question #63 : Unit Circle And Radians

Example Question #24 : Radians

Example Question #63 : Unit Circle And Radians

Example Question #64 : Unit Circle And Radians

Example Question #443 : Trigonometry

Example Question #4 : Angles In The Unit Circle

Example Question #5 : Angles In The Unit Circle

All Trigonometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: