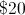SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)
Study concepts, example questions & explanations for SSAT Upper Level Math
All SSAT Upper Level Math Resources
Example Questions
Example Question #1121 : Ssat Upper Level Quantitative (Math)
Evan wants to tip approximately 
The tab can be rounded to 
Now we can multiply the percent by the total amount.
Example Question #2 : How To Estimate
If the number 
If 
Given that 
Example Question #1 : Estimation
Estimate the product 
437 rounded to the nearest hundred is 400.
877 rounded to the nearest hundred is 900.
551 rounded to the nearest hundred is 600.
Multiply the three whole multiples of 100 to get the desired estimate:
Example Question #2 : How To Estimate
Estimate the product 
Multiply the three whole numbers to get the desired estimate:
Example Question #1122 : Ssat Upper Level Quantitative (Math)
Estimate the result 
8.19 rounded to the nearest unit is 8.
4.87 rounded to the nearest unit is 5
3.27 rounded to the nearest unit is 3.
7.42 rounded to the nearest unit is 7.
The desired estimate can be found as follows:
Example Question #4 : How To Estimate
Estimate the result 
The desired estimate can be found as follows:
Example Question #1123 : Ssat Upper Level Quantitative (Math)
Melissa is trying to come up with a reasonable estimate of the amount she spent on groceries over the last six months. She notices that the six checks she wrote out to the local grocery store are in the following amounts: $187.54, $218.89, $174.74, $104.76, $189.75, and $228.64. By estimating each of the amounts of the checks to the nearest ten dollars, come up with a reasonable estimate for Melissa's total expenditure for groceries.
Round each of the amounts to the nearest ten dollars as follows:
$187.54 rounds to $190.
$218.89 rounds to $220.
$174.74 rounds to $170.
$104.76 rounds to $100.
$189.75 rounds to $190.
$228.64 rounds to $230.
Add the rounded figures:
Example Question #1124 : Ssat Upper Level Quantitative (Math)
Estimate the product 
8.39 rounded to the nearest unit is 8 because 0.39 is less than 0.5.
7.34 rounded to the nearest unit is 7 because 0.34 is less than 0.5.
3.52 rounded to the nearest unit is 4 because 0.52 is greater than 0.5.
Multiply the three whole numbers to get the desired estimate:
Example Question #1 : Proportion / Ratio / Rate
A barn has 
First, add up the total number of ducks, geese, and chickens.
Now, write the fraction of these animals that are geese and the fraction of these animals that are chickens.
Now, since we want the ratio of geese to chickens, we write the fractions as thus:
Divide and simplify the resulting fraction to find the ratio.
Example Question #1 : Proportion / Ratio / Rate
If 
There is more than one way to solve this problem. You can either figure out how much the chicken costs per pound and multiply that cost by three pounds, or you can set up a proportion and solve for the cost of three pounds of chicken that way.
1) Solving the Problem Using Cost per Pound
First, find how much the chicken costs per pound.
Since chicken costs 
2) Solving the Problem Using a Proportion
You can set up a proportion to figure out how much 
Cross multiply:
Solve for 
All SSAT Upper Level Math Resources
