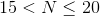We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Rational Numbers

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #12 : How To Find Decimal Fractions

Convert to a fraction.

$3*10^{-4}$

Possible Answers:

$\frac{3}{100000}$

$\frac{3}{10000}$

$\frac{3}{1000}$

$\frac{3}{10000000}$

$\frac{3}{100}$

Correct answer:

$\frac{3}{10000}$

Explanation:

First, lets convert the exponent into a fraction. Any negative exponent means it's the reciprocal of the positive exponent. So $10^{-4}$ means $\frac{1}{10^{4}}$ . Now lets multiply it with the . This means $3*\frac{1}{10^4}$ or $3*\frac{1}{10000}$ or $\frac{3}{10000}$ .

Report an Error

Example Question #12 : How To Find Decimal Fractions

Convert 0.33333333333.... into a fraction.

Possible Answers:

$\frac{33333}{100000}$

$\frac{33333333333333}{100000000000000}$

$\frac{333}{1000}$

$\frac{33}{100}$

$\frac{1}{3}$

Correct answer:

$\frac{1}{3}$

Explanation:

Let 0.33333333333.... be . (0.33333333333=x)

Lets multiply by . Now we have:

3.33333333333= 10x

Lets subtract this equation with the first one and we get:

9x=3 We do this because we want to get rid of the repeating decimals and now we have a simple equation, isolate and we arrive at the final answer.

Report an Error

Example Question #283 : Fractions

Convert 0.857857857857... into a fraction.

Possible Answers:

$\frac{857}{1000}$

$\frac{8}{9}$

$\frac{857}{999}$

$\frac{7}{9}$

$\frac{857}{998}$

Correct answer:

$\frac{857}{999}$

Explanation:

Let 0.857857857... be . (0.857857857...=x)

Lets multiply by 1000 . I chose 1000 , because there is a set of numbers that make the repeating decimal. To determine the value to multiply the repeating decimal, we do to the power of number in a set before it repeats.

Now we have:

857.857857857...=1000x

Lets subtract this equation with the first one and we get:

999x=857 We do this because we want to get rid of the repeating decimals and now we have a simple equation, isolate and we arrive at the final answer.

Report an Error

Example Question #1 : Simplifying Fractions

Rewrite the mixed fraction $6\frac{12}{15}$ as an improper fraction in lowest terms, and call the product of the numerator and the denominator of the simplified improper fraction. How many digits does have?

Possible Answers:

Correct answer:

Explanation:

$\frac{12}{15} = \frac{12 \div 3}{15 \div 3} = \frac{4}{5}$ , so $6\frac{12}{15}$ simplifies to $6\frac{4}{5}$ .

The numerator of the improper form of a mixed fraction is the original numerator added to the product of the integer and the original denominator. The new denominator is the same as the old one. Therefore,

$6\frac{4}{5} = \frac{6 \times 5 + 4}{5} = \frac{30+4}{5} = \frac{34}{5}$

Multiply the numerator and the denominator: $34 \times 5 = 170$ ,

a three-digit number.

Report an Error

Example Question #2 : Simplifying Fractions

Reduce $\frac{16}{60}$ to lowest terms, call the sum of the numerator and the denominator. Which statement is true of ?

Possible Answers:

$30 < N \le 35$

$20 < N \le 25$

$25 < N \le 30$

$15 < N \le 20$

$10 < N \le 15$

Correct answer:

$15 < N \le 20$

Explanation:

$\frac{16}{60} = \frac{16 \div 4}{60 \div 4} = \frac{4}{15}$

Add the numerator and the denominator: 4+15= 19

The correct response is therefore $15 < N \le 20$ .

Report an Error

Example Question #3 : Simplifying Fractions

Consider a fraction $\frac{N}{65}$ , where the numerator is unknown. How many of the following values of would yield a fraction not in lowest terms?

I) N = 115

II) N = 116

III) N = 117

IV) N = 118

Possible Answers:

$\textup{Two}$

$\textup{Three}$

$\textup{Four}$

$\textup{One}$

$\textup{None}$

Correct answer:

$\textup{Two}$

Explanation:

The prime factorization of is $5 \times 13$ , so the fraction $\frac{N}{65}$ is reducible if and only if is a multiple of 5 or 13.

We can immediately tell that 115 is the only multiple of 5, so we test the other numbers to see if there is a multiple of 13. We soon see that

$117 \div 13 = 9$ , so 116 and 118 cannot be multples of 13.

115 and 117 are the only values of that yield reducible fractions, so the correct response is two.

Report an Error

Example Question #2 : Simplifying Fractions

Reduce the fraction $\frac{39}{111}$ to lowest terms, and call the product of the numerator and the denominator of the simplified fraction. Give the value of .

Possible Answers:

507

481

$\text{The correct answer is not among the other choices.}$

429

444

Correct answer:

481

Explanation:

$\frac{39 \div 3}{111 \div 3} = \frac{13}{37}$

Multiply the numerator and the denominator: $13 \times 37 = 481$

The product is a three-digit number.

Report an Error

Example Question #1413 : Ssat Upper Level Quantitative (Math)

Put the fraction in the simplest form.

$\frac{24}{36}$

Possible Answers:

$\frac{2}{3}$

$\frac{12}{18}$

$\frac{4}{6}$

$\frac{8}{12}$

Correct answer:

$\frac{2}{3}$

Explanation:

To put a fraction in simplest form, keep dividing the numerator and denominator by the same number until you cannot go any further.

$\frac{24\div2}{36\div2}=\frac{12}{18}$

$\frac{12\div2}{18\div2}=\frac{6}{9}$

$\frac{6\div3}{9\div3}=\frac{2}{3}$

Report an Error

Example Question #1 : How To Simplify A Fraction

Put the fraction in simplest form.

$\frac{224}{400}$

Possible Answers:

$\frac{28}{50}$

$\frac{56}{100}$

$\frac{14}{25}$

$\frac{25}{14}$

Correct answer:

$\frac{14}{25}$

Explanation:

To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.

$\frac{224\div4}{400\div4}=\frac{56\div2}{100\div2}=\frac{28\div2}{50\div2}=\frac{14}{25}$

Report an Error

Example Question #281 : Rational Numbers

Put the fraction in simplest form.

$\frac{36}{120}$

Possible Answers:

$\frac{3}{120}$

$\frac{6}{20}$

$\frac{3}{10}$

$\frac{10}{3}$

Correct answer:

$\frac{3}{10}$

Explanation:

To simplify a fraction, divide both the numerator and the denominator by the same numbers until there is no number that can divide them both without resulting in a remainder.

$\frac{36 \div 12}{120 \div 12}=\frac{3}{10}$

Report an Error

View SSAT- Upper Level Tutors

Denisha
Certified Tutor

Nova Southeastern University, Doctor of Medicine, Ayurvedic Medicine. Nova Southeastern University, Master in Public Health, ...

View SSAT- Upper Level Tutors

Wardell
Certified Tutor

SIU Edwardsville, Bachelor in Arts, English.

View SSAT- Upper Level Tutors

Marlene
Certified Tutor

Herbert Lehman, Bachelors, Recreation Education. Long Island University-Brooklyn Campus, Masters, Special Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Miami, Math Tutors in Seattle, Reading Tutors in San Francisco-Bay Area, Statistics Tutors in San Francisco-Bay Area, Spanish Tutors in Washington DC, Reading Tutors in Philadelphia, English Tutors in San Francisco-Bay Area, Math Tutors in Los Angeles, Algebra Tutors in Miami, SSAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Atlanta, GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Atlanta, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Washington DC, ISEE Courses & Classes in Miami, SAT Courses & Classes in Los Angeles, SAT Courses & Classes in Denver, LSAT Courses & Classes in Philadelphia

Popular Test Prep

GRE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Phoenix, LSAT Test Prep in Houston, MCAT Test Prep in New York City, ISEE Test Prep in Denver, GRE Test Prep in Dallas Fort Worth, GRE Test Prep in Denver, GMAT Test Prep in Washington DC, MCAT Test Prep in Phoenix, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Rational Numbers

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #12 : How To Find Decimal Fractions

Example Question #12 : How To Find Decimal Fractions

Example Question #283 : Fractions

Example Question #1 : Simplifying Fractions

Example Question #2 : Simplifying Fractions

Example Question #3 : Simplifying Fractions

Example Question #2 : Simplifying Fractions

Example Question #1413 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Simplify A Fraction

Example Question #281 : Rational Numbers

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: