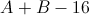All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : Midpoint Formula
A line segment on the coordinate plane has midpoint 




Let 


Example Question #2 : Midpoint Formula
A line segment on the coordinate plane has one endpoint at 




To find the value of the 



We solve for 
Example Question #1 : How To Find The Endpoints Of A Line Segment
One endpoint of a line segment on the coordinate plane is the point 


In the 

set 
This is the correct 
Example Question #2 : How To Find The Endpoints Of A Line Segment
One endpoint of a line segment on the coordinate plane is the point 


Using the 

set 
The second endpoint is 
Example Question #124 : Lines
On the coordinate plane, 







Give the 

First, find the 



set 
Now, find the 

This is the correct response.
Example Question #4 : How To Find The Endpoints Of A Line Segment
On the coordinate plane, 







Give the 

First, find the 



set 
Now, find the 

This is the correct response.
Example Question #1 : How To Find The Endpoints Of A Line Segment
On the coordinate plane, 







Give the 

First, find the 



set 
Now, find the 

This is the correct response.
Example Question #1 : How To Find The Endpoints Of A Line Segment
On the coordinate plane, 







Give the 

First, find the 




set 
Now, find the 

This is the correct response.
All SSAT Upper Level Math Resources