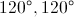Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find an angle in a right triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find An Angle In A Right Triangle

One angle of a right triangle has measure $120^{\circ }$ $\displaystyle 120^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

$90^{\circ }, 120^{\circ }$ $\displaystyle 90^{\circ }, 120^{\circ }$

$30^{\circ }, 90^{\circ }$ $\displaystyle 30^{\circ }, 90^{\circ }$

$30^{\circ }, 30^{\circ }$ $\displaystyle 30^{\circ }, 30^{\circ }$

This triangle cannot exist.

$120^{\circ }, 120^{\circ }$ $\displaystyle 120^{\circ }, 120^{\circ }$

Correct answer:

This triangle cannot exist.

Explanation:

A right triangle must have one right angle and two acute angles; this means that no angle of a right triangle can be obtuse. But since $120^{\circ } > 90^{\circ }$ $\displaystyle 120^{\circ } > 90^{\circ }$ , it is obtuse. This makes it impossible for a right triangle to have a $120^{\circ }$ $\displaystyle 120^{\circ }$ angle.

Report an Error

Example Question #1 : How To Find An Angle In A Right Triangle

One angle of a right triangle has measure $68^{\circ }$ $\displaystyle 68^{\circ }$ . Give the measures of the other two angles.

Possible Answers:

$44^{\circ },68^{\circ }$ $\displaystyle 44^{\circ },68^{\circ }$

$56^{\circ },56^{\circ }$ $\displaystyle 56^{\circ },56^{\circ }$

$22^{\circ }, 90^{\circ }$ $\displaystyle 22^{\circ }, 90^{\circ }$

$52^{\circ }, 60^{\circ }$ $\displaystyle 52^{\circ }, 60^{\circ }$

This triangle cannot exist.

Correct answer:

$22^{\circ }, 90^{\circ }$ $\displaystyle 22^{\circ }, 90^{\circ }$

Explanation:

One of the angles of a right triangle is by definition a right, or $90^{\circ }$ $\displaystyle 90^{\circ }$ , angle, so this is the measure of one of the missing angles. Since the measures of the angles of a triangle total $180^{\circ }$ $\displaystyle 180^{\circ }$ , if we let the measure of the third angle be $\displaystyle x$ , then:

$\displaystyle x + 68 + 90 = 180$

$\displaystyle x + 158 = 180$

$\displaystyle x + 158 - 158= 180 - 158$

x = 22 $\displaystyle x = 22$

The other two angles measure $22 ^{\circ }, 90^{\circ }$ $\displaystyle 22 ^{\circ }, 90^{\circ }$ .

Report an Error

Example Question #2 : How To Find An Angle In A Right Triangle

Find the degree measure of $\displaystyle x$ in the right triangle below.

Possible Answers:

$47^{\circ}$ $\displaystyle 47^{\circ}$

$90^{\circ}$ $\displaystyle 90^{\circ}$

$32^{\circ}$ $\displaystyle 32^{\circ}$

$43^{\circ}$ $\displaystyle 43^{\circ}$

Correct answer:

$43^{\circ}$ $\displaystyle 43^{\circ}$

Explanation:

The total number of degrees in a triangle is 180 $\displaystyle 180$ .

While $47^{\circ}$ $\displaystyle 47^{\circ}$ is provided as the measure of one of the angles in the diagram, you are also told that the triangle is a right triangle, meaning that it must contain a $90^{\circ}$ $\displaystyle 90^{\circ}$ angle as well. To find the value of $\displaystyle x$ , subtract the other two degree measures from 180 $\displaystyle 180$ .

$x=180-90-47=43^{\circ}$ $\displaystyle x=180-90-47=43^{\circ}$

Report an Error

Example Question #51 : Properties Of Triangles

Find the angle value of $\displaystyle v$ .

Possible Answers:

$47^{\circ}$ $\displaystyle 47^{\circ}$

$43^{\circ}$ $\displaystyle 43^{\circ}$

$53^{\circ}$ $\displaystyle 53^{\circ}$

$90^{\circ}$ $\displaystyle 90^{\circ}$

Correct answer:

$43^{\circ}$ $\displaystyle 43^{\circ}$

Explanation:

All the angles in a triangle must add up to 180 degrees.

$90^{\circ}+47^{\circ}+v=180^{\circ}$ $\displaystyle 90^{\circ}+47^{\circ}+v=180^{\circ}$

$137^{\circ}+v=180^{\circ}$ $\displaystyle 137^{\circ}+v=180^{\circ}$

$137^{\circ}+v-137^{\circ}=180^{\circ}-137^{\circ}$ $\displaystyle 137^{\circ}+v-137^{\circ}=180^{\circ}-137^{\circ}$

$v=43^{\circ}$ $\displaystyle v=43^{\circ}$

Report an Error

Example Question #5 : How To Find An Angle In A Right Triangle

Find the angle value of $\displaystyle w$ .

Possible Answers:

$48^{\circ}$ $\displaystyle 48^{\circ}$

$68^{\circ}$ $\displaystyle 68^{\circ}$

$38^{\circ}$ $\displaystyle 38^{\circ}$

$58^{\circ}$ $\displaystyle 58^{\circ}$

Correct answer:

$58^{\circ}$ $\displaystyle 58^{\circ}$

Explanation:

All the angles in a triangle adds up to $180^{\circ}$ $\displaystyle 180^{\circ}$ .

$90^{\circ}+32^{\circ}+w=180^{\circ}$ $\displaystyle 90^{\circ}+32^{\circ}+w=180^{\circ}$

$122^{\circ}+w=180^{\circ}$ $\displaystyle 122^{\circ}+w=180^{\circ}$

$122^{\circ}+w-122^{\circ}=180^{\circ}-122^{\circ}$ $\displaystyle 122^{\circ}+w-122^{\circ}=180^{\circ}-122^{\circ}$

$w=58^{\circ}$ $\displaystyle w=58^{\circ}$

Report an Error

Example Question #6 : How To Find An Angle In A Right Triangle

Find the angle value of $\displaystyle y$ .

Possible Answers:

$36^{\circ}$ $\displaystyle 36^{\circ}$

$66^{\circ}$ $\displaystyle 66^{\circ}$

$46^{\circ}$ $\displaystyle 46^{\circ}$

$56^{\circ}$ $\displaystyle 56^{\circ}$

Correct answer:

$46^{\circ}$ $\displaystyle 46^{\circ}$

Explanation:

All the angles in a triangle add up to 180 $\displaystyle 180$ degrees.

$90^{\circ}+44^{\circ}+y=180^{\circ}$ $\displaystyle 90^{\circ}+44^{\circ}+y=180^{\circ}$

$134^{\circ}+y=180^{\circ}$ $\displaystyle 134^{\circ}+y=180^{\circ}$

$134^{\circ}+y-134^{\circ}=180^{\circ}-134^{\circ}$ $\displaystyle 134^{\circ}+y-134^{\circ}=180^{\circ}-134^{\circ}$

$y=46^{\circ}$ $\displaystyle y=46^{\circ}$

Report an Error

Example Question #52 : Right Triangles

Find the angle measure of $\displaystyle z$ .

Possible Answers:

$41^{\circ}$ $\displaystyle 41^{\circ}$

$31^{\circ}$ $\displaystyle 31^{\circ}$

$51^{\circ}$ $\displaystyle 51^{\circ}$

$21^{\circ}$ $\displaystyle 21^{\circ}$

Correct answer:

$31^{\circ}$ $\displaystyle 31^{\circ}$

Explanation:

All the angles in a triangle add up to $180^{\circ}$ $\displaystyle 180^{\circ}$ .

$90^{\circ}+59^{\circ}+z=180^{\circ}$ $\displaystyle 90^{\circ}+59^{\circ}+z=180^{\circ}$

$149^{\circ}+z=180^{\circ}$ $\displaystyle 149^{\circ}+z=180^{\circ}$

$149^{\circ}+z-149^{\circ}=180^{\circ}-149^{\circ}$ $\displaystyle 149^{\circ}+z-149^{\circ}=180^{\circ}-149^{\circ}$

$z=31^{\circ}$ $\displaystyle z=31^{\circ}$

Report an Error

View SSAT- Upper Level Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View SSAT- Upper Level Tutors

Rose
Certified Tutor

Texas A & M University-Corpus Christi, Associate in Science, Elementary School Teaching. Walden University, Masters in Educat...

View SSAT- Upper Level Tutors

Colin
Certified Tutor

Cooper Union for the Advancement of Science and Art, Bachelor of Fine Arts, Fine and Studio Arts Management. The University o...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Seattle, French Tutors in Boston, Chemistry Tutors in Miami, MCAT Tutors in Dallas Fort Worth, LSAT Tutors in Chicago, ISEE Tutors in Philadelphia, Statistics Tutors in Seattle, English Tutors in Atlanta, Statistics Tutors in Dallas Fort Worth, Statistics Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Miami, GMAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in Chicago, SAT Courses & Classes in Denver, Spanish Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Boston

Popular Test Prep

GMAT Test Prep in Philadelphia, GRE Test Prep in Houston, GRE Test Prep in New York City, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Seattle, MCAT Test Prep in Washington DC, ISEE Test Prep in New York City, SAT Test Prep in Los Angeles, SAT Test Prep in New York City, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find an angle in a right triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : How To Find An Angle In A Right Triangle

Example Question #1 : How To Find An Angle In A Right Triangle

Example Question #2 : How To Find An Angle In A Right Triangle

Example Question #51 : Properties Of Triangles

Example Question #5 : How To Find An Angle In A Right Triangle

Example Question #6 : How To Find An Angle In A Right Triangle

Example Question #52 : Right Triangles

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: