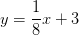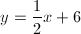All SSAT Upper Level Math Resources
Example Questions
Example Question #9 : How To Find The Slope Of Parallel Lines
Which of the following is a line that is parallel to the line 
For a given line 



Example Question #10 : How To Find The Slope Of Parallel Lines
What is the slope of the line 
In order to most easily determine the slope, let's turn this equation into its slope-intercept form 
We can start by subtracting 

Then, we can divide the entire equation by 

Therefore, 
Example Question #1 : How To Find The Equation Of A Parallel Line
Which of the following equations gives a line that is parallel to the line with the equation 
Two lines are parallel when they have the same slope. Because the slope of the given line is 



Example Question #161 : Lines
A line has the equation 

The slope of the second line must be 
To find the equation of this second line, just plug in the given point into the standard form 

Now we have all the parts needed to write the equation for the second line:
Example Question #3 : How To Find The Equation Of A Parallel Line
Line 





Since lines 






Thus, the equation of line 
Example Question #1 : How To Find The Equation Of A Parallel Line
There is a line defined by the equation below:
There is a second line that passes through the point 
Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.
3x + 4y = 12
4y = –3x + 12
y = –(3/4)x + 3
slope = –3/4
We know that the second line will also have a slope of –3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.
y = mx + b
2 = –3/4(1) + b
2 = –3/4 + b
b = 2 + 3/4 = 2.75
Plug the y-intercept back into the equation to get our final answer.
y = –(3/4)x + 2.75
Example Question #2 : Coordinate Geometry
What is the equation of a line that is parallel to 

To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.
The slope of the line will be 

The final equation for the line will be 
Example Question #2 : How To Find The Equation Of A Parallel Line
What line is parallel to 

Start by converting the original equation to slop-intercept form.
The slope of this line is 
Plug the y-intercept into the slope-intercept equation to get the final answer.
Example Question #3 : Coordinate Geometry
What is the equation of a line that is parallel to the line 

The line parallel to 



Therefore, the equation of the line is 
Example Question #3 : How To Find The Equation Of A Parallel Line
What line is parallel to 

Converting the given line to slope-intercept form we get the following equation:
For parallel lines, the slopes must be equal, so the slope of the new line must also be 
Use the y-intercept in the slope-intercept equation to find the final answer.
Certified Tutor
All SSAT Upper Level Math Resources