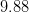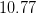All SSAT Upper Level Math Resources
Example Questions
Example Question #8 : How To Find The Equation Of A Perpendicular Line
Given a line 


For a given line 





In this instance, the slope of line 



Example Question #9 : How To Find The Equation Of A Perpendicular Line
A given line 


Not enough information provided
For a given line 





Since in this case 

Example Question #81 : Coordinate Geometry
Which of the following equations represents a line that goes through the point 

In order to solve this problem, we need first to transform the equation from standard form to slope-intercept form:
Transform the original equation to find its slope.

First, subtract 
Simplify and rearrange.

Next, divide both sides of the equation by 6.
The slope of our first line is equal to 
Let's calculate the opposite reciprocal of our slope:
The slope of our line is equal to 2. We now have the following partial equation:
We are missing the y-intercept, 


Add 4 to both sides of the equation.
Substitute this value into our partial equation to construct the equation of our line:
Example Question #91 : Lines
A line segment has the endpoints 

Use the following formula to find the distance between two points:
Plug in the points that are given.
Example Question #1 : How To Find The Length Of A Line With Distance Formula
A line segment has end points at 

The distance between two points is given by the following equation:
Now, using the two given points, plug them in to find the distance.
Example Question #2 : Distance Formula
Find the length of a line that has end points at 
Use the distance formula to find the length of this line segment:
Substitute in the values provided:
At this point, break down the square root:
You can remove two of the twos and put them on the outside of the square root symbol, and multiply the two and the thirteen that remain underneath the square root symbol:
Example Question #371 : Ssat Upper Level Quantitative (Math)
A line segment has endpoints at 
Use the distance formula to find the length of the line segment.
Where,


Example Question #1 : Distance Formula
Find the length of the line segment that has endpoints 
Use the distance formula to find the length of the line segment.
Where,


Example Question #6 : Distance Formula
Find the length of the line segment that has the endpoints 
Use the distance formula to find the length of the line.
Where,


Example Question #7 : Distance Formula
One leg of a triangle has endpoints at the coordinates 
Use the distance formula to find the length of the leg.
Where,


Certified Tutor
All SSAT Upper Level Math Resources