We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : SSAT Middle Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : Area Of A Triangle

A triangle has a height of 9 inches and a base that is one third as long as the height. What is the area of the triangle, in square inches?

Possible Answers:

$\frac{27}{2}$

None of these

Correct answer:

$\frac{27}{2}$

Explanation:

The area of a triangle is found by multiplying the base times the height, divided by 2.

$\text{Area} =\frac{\text{base}\times \text{height}}{2}$

Given that the height is 9 inches, and the base is one third of the height, the base will be 3 inches.

$b=h\div3=9\div3=3$

We now have both the base (3) and height (9) of the triangle. We can use the equation to solve for the area.

$\text{Area} =\frac{9\times 3}{2}$

$\text{Area} =\frac{27}{2}$

The fraction cannot be simplified.

Report an Error

Example Question #51 : Geometry

The hypotenuse of a right triangle is feet; it has one leg feet long. Give its area in square inches.

Possible Answers:

$101,088 \textrm{ in}^{2}$

$77,760 \textrm{ in}^{2}$

$38,880 \textrm{ in}^{2}$

$43,120 \textrm{ in}^{2}$

$42,120 \textrm{ in}^{2}$

Correct answer:

$38,880 \textrm{ in}^{2}$

Explanation:

The area of a right triangle is half the product of the lengths of its legs, so we need to use the Pythagorean Theorem to find the length of the other leg. Set c = 39 , b = 36 :

$a^{2} = c^{2} - b^{2}$

$a^{2} = 39 ^{2} - 36^{2}$

$a^{2} = 1,521 - 1,296$

$a^{2} = 225$

$a = \sqrt{225} = 15$

The legs have length and feet; multiply both dimensions by to convert to inches:

$15 \times 12 = 180$ inches

$36 \times 12 = 432$ inches.

Now find half the product:

$A = \frac{1}{2} \cdot 180 \cdot 432 = 38,880\ in^{2}$

Report an Error

Example Question #101 : Geometry

What is the area (in square feet) of a triangle with a base of feet and a height of feet?

Possible Answers:

Correct answer:

Explanation:

The area of a triangle is found by multiplying the base times the height, divided by .

$Area =\frac{base\cdot height}{2}$

$Area =\frac{4\cdot 7}{2}$

Area=14

Report an Error

Example Question #11 : Triangles

What is the area of a triangle with a base of and a height of ?

Possible Answers:

Correct answer:

Explanation:

The formula for the area of a triangle is $\dpi{100} Area=\frac{1}{2}\times base\times height$ .

Plug the given values into the formula to solve:

$\dpi{100} Area=\frac{1}{2}\times 12\times 3$

$\dpi{100} Area=\frac{1}{2}\times 36$

$\dpi{100} Area=18$

Report an Error

Example Question #15 : How To Find The Area Of A Triangle

Right triangle 2

Give the perimeter of the above triangle in feet.

Possible Answers:

$2 \frac{2}{3}\textrm{ ft }$

$3 \frac{1}{3}\textrm{ ft }$

$3 \frac{1}{2}\textrm{ ft }$

$2 \frac{1}{2}\textrm{ ft }$

Correct answer:

$2 \frac{1}{2}\textrm{ ft }$

Explanation:

The perimeter of the triangle - the sum of the lengths of its sides - is

5 + 12 + 13 = 30 inches.

Divide by 12 to convert to feet:

$30 \div 12 = 2 \textrm{ R }6$

As a fraction, this is $2 \frac{6}{12}$ or $2 \frac{1}{2}$ feet,

Report an Error

Example Question #11 : Plane Geometry

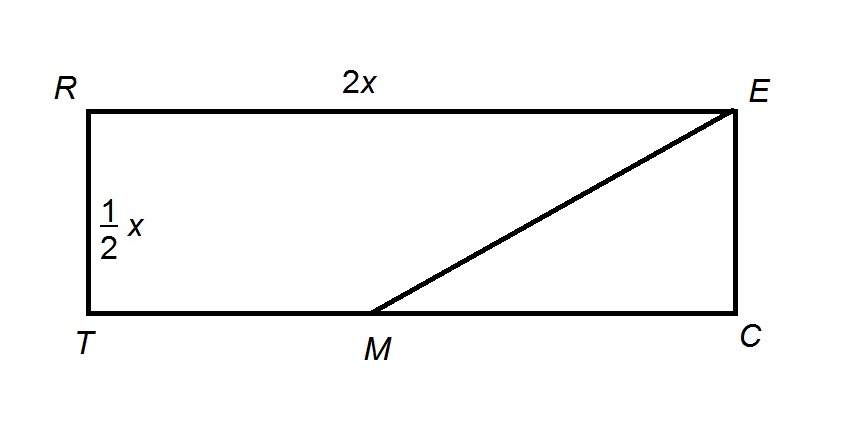
Rectangles 3

The above diagram shows Rectangle RECT , with midpoint of $\overline{CT}$ .

The area of $\bigtriangleup ECM$ is 225. Evaluate

Possible Answers:

Correct answer:

Explanation:

is the midpoint of $\overline{CT}$ , so $\bigtriangleup ECM$ has as its base $CM= \frac{1}{2} \cdot CT = \frac{1}{2} \cdot 2x =x$ ; its height is $EC = \frac{1}{2} x$ .

Its area is half their product, or

$\frac{1}{2} \cdot x \cdot \frac{1}{2} x = \frac{1}{4} x^{2}$

Set this equal to 225:

$\frac{1}{4} x^{2} = 225$

$4 \cdot \frac{1}{4} x^{2} = 4 \cdot 225$

$x^{2} = 900$

$x = \sqrt{900}= 30$ .

Report an Error

Example Question #17 : Plane Geometry

Find the area of a triangle with a height of 12in and a base that is half the height.

Possible Answers:

$30\text{in}^2$

$6\text{in}^2$

$18\text{in}^2$

$24\text{in}^2$

$36\text{in}^2$

Correct answer:

$36\text{in}^2$

Explanation:

To find the area of a triangle, we will use the following formula:

$A = \frac{1}{2} \cdot b \cdot h$

where b is the base and h is the height of the triangle.

Now, we know the height of the triangle is 12in. We also know the base of the triangle is half of the height. Therefore, the base of the triangle is 6in.

So, we can substitute. We get

$A = \frac{1}{2} \cdot 6\text{in} \cdot 12\text{in}$

$A = 3\text{in} \cdot 12\text{in}$

$A = 36\text{in}^2$

Report an Error

Example Question #21 : Plane Geometry

Find the area of the triangle below

Screen shot 2015 11 10 at 9.45.10 pm

Possible Answers:

$21 \frac{1}{3}$

Correct answer:

Explanation:

The equation for area of a triangle is

$\frac{b\times h}{2}$ .

In this case the coordinates of the base are (-3,0)(5,0) , which means the length of the base is 5--3=8 .

The coordinates of the side that determines the height are (-3,0)(-3,8) .

Therefore the height is 8-0=8 .

$\frac{8\times8}{2}=\frac{64}{2}=32$ .

Report an Error

Example Question #1 : How To Find Perimeter Of A Triangle

The perimeter of an isosceles triangle is 18. What is a possible list of the lengths of the sides?

Possible Answers:

5,5,7

5,6,7

4,5,9

5,5,8

4,4,11

Correct answer:

5,5,8

Explanation:

Since it is isosceles, 2 of the sides must be equal. They must also add to 18.

Report an Error

Example Question #2 : How To Find Perimeter Of A Triangle

An equilateral triangle has perimeter 8 feet 6 inches. How long is one side?

Possible Answers:

3 feet 4 inches

3 feet 2 inches

2 feet 2 inches

2 feet 6 inches

2 feet 10 inches

Correct answer:

2 feet 10 inches

Explanation:

One foot is equal to 12 inches, so the perimeter 8 feet 6 inches is equal to $8 \times 12 + 6 = 96 + 6 = 102$ inches.

An equilateral triangle has three sides of equal measure, so divide its perimeter by 3:

$102 \div 3 = 34$

To convert 34 inches to feet and inches:

$34\div 12 = 2 \textrm{ R }10$

One side measures 2 feet 10 inches.

Report an Error

View SSAT- Middle Level Tutors

Denisha
Certified Tutor

Nova Southeastern University, Doctor of Medicine, Ayurvedic Medicine. Nova Southeastern University, Master in Public Health, ...

View SSAT- Middle Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

View SSAT- Middle Level Tutors

Adam
Certified Tutor

University of Mary Washington, Bachelor in Arts, Cultural Anthropology. George Mason University, Masters in Education, Educat...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Chicago, Math Tutors in Miami, ISEE Tutors in San Diego, MCAT Tutors in Miami, SAT Tutors in Washington DC, Biology Tutors in San Francisco-Bay Area, Reading Tutors in New York City, Calculus Tutors in Houston, Statistics Tutors in New York City, SSAT Tutors in Washington DC

Popular Courses & Classes

ACT Courses & Classes in Miami, SAT Courses & Classes in Phoenix, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in Washington DC, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Denver, MCAT Courses & Classes in Boston, SAT Courses & Classes in Houston

Popular Test Prep

GMAT Test Prep in Houston, SSAT Test Prep in Denver, SAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Houston, GMAT Test Prep in Miami, MCAT Test Prep in New York City, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : SSAT Middle Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #4 : Area Of A Triangle

Example Question #51 : Geometry

Example Question #101 : Geometry

Example Question #11 : Triangles

Example Question #15 : How To Find The Area Of A Triangle

Example Question #11 : Plane Geometry

Example Question #17 : Plane Geometry

Example Question #21 : Plane Geometry

Example Question #1 : How To Find Perimeter Of A Triangle

Example Question #2 : How To Find Perimeter Of A Triangle

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: