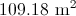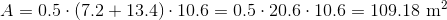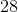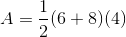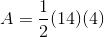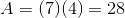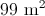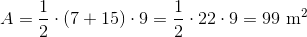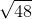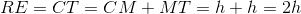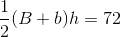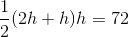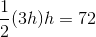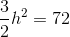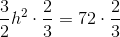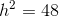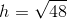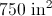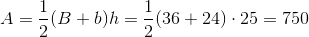We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Trapezoids

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

Find the area of the trapezoid above.

Note: Image not drawn to scale.

Possible Answers:

$80\: cm$

$200\: cm^{2}$

$120\: cm^{2}$

$160\: cm$

$120\: cm$

Correct answer:

$120\: cm^{2}$

Explanation:

The area of a trapezoid is equal to the average of the length of the two bases multiplied by the height.

The formula to find the area of a trapezoid is: $\left (\frac{base_{1} + base_{2}}{2}\right )* height$

In this problem, the lengths of the bases are $10\: cm$ and $20\: cm.$ Their average is $15\: cm$ . The height of the trapezoid is $8\: cm.$

$15\: cm\ast 8\: cm=120\: cm$

Remember: the answer to the problem should have units in cm² .

Report an Error

Example Question #3 : How To Find The Area Of A Trapezoid

Find the area of a trapezoid with a height of $5\:cm$ and base lengths of $4\:cm$ and $8\:cm$ , respectively.

Possible Answers:

$17\:cm$

$15\:cm^{2}$

$22\:cm^{2}$

$30\:cm^{2}$

$10\:cm^{2}$

Correct answer:

$30\:cm^{2}$

Explanation:

The area of a trapezoid is equal to the average of its two bases ( $b_{1}$ and $b_{2}$ ) multiplied by its height . Therefore:

$A=\frac{1}{2}(b_{1}+b_{2})h$

$A=\frac{1}{2}(4\:cm+8\:cm)5\:cm$

$A=\(6\:cm)5\:cm$

$A=30\:cm^{2}$

Report an Error

Example Question #3 : How To Find The Area Of A Trapezoid

Find the area of a trapezoid with a height of $8\:cm$ and base lengths of $10\:cm$ and $12\:cm$ , respectively.

Possible Answers:

$30\:cm$

$30\:cm^{2}$

$88\:cm$

$52\:cm^{2}$

$88\:cm^{2}$

Correct answer:

$88\:cm^{2}$

Explanation:

The area of a trapezoid is equal to the average of its two bases ( $b_{1}$ and $b_{2}$ ) multiplied by its height . Therefore:

$A=\frac{1}{2}(b_{1}+b_{2})h$

$A=\frac{1}{2}(10\:cm+12\:cm)8\:cm$

$A=\(11\:cm)8\:cm$

$A=88\:cm^{2}$

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

Trapezoid

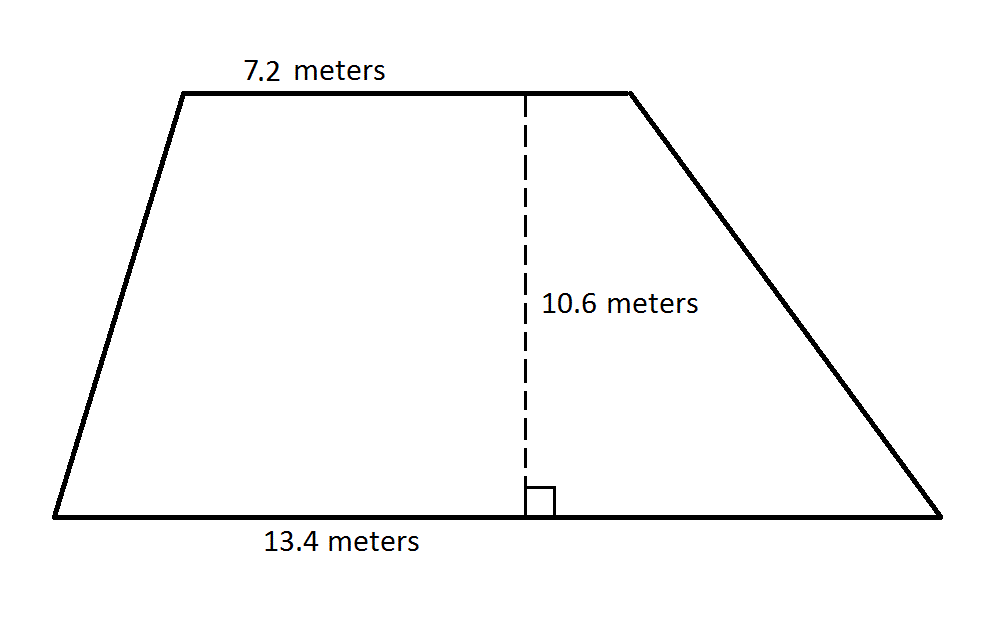
What is the area of the above trapezoid?

Possible Answers:

$96.48\textrm{ m}^{2}$

$218.36\textrm{ m}^{2}$

$109.18\textrm{ m}^{2}$

$142.04\textrm{ m}^{2}$

$76.32\textrm{ m}^{2}$

Correct answer:

$109.18\textrm{ m}^{2}$

Explanation:

To find the area of a trapezoid, multiply one half (or 0.5, since we are working with decimals) by the sum of the lengths of its bases (the parallel sides) by its height (the perpendicular distance between the bases). This quantity is

$A = 0.5 \cdot (7.2 + 13.4) \cdot 10.6 =0.5 \cdot 20.6 \cdot 10.6 = 109.18\textrm{ m}^{2}$

Report an Error

Example Question #131 : Quadrilaterals

Find the area of the trapezoid:

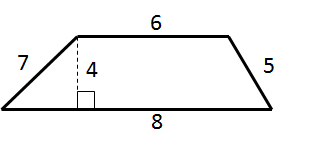
Question_7

Possible Answers:

Correct answer:

Explanation:

The area of a trapezoid can be determined using the equation $A=\frac{1}{2}(b_1+b_2)h$ .

$A=\frac{1}{2}(6+8)(4)$

$A=\frac{1}{2}(14)(4)$

A=(7)(4)=28

Report an Error

Example Question #132 : Quadrilaterals

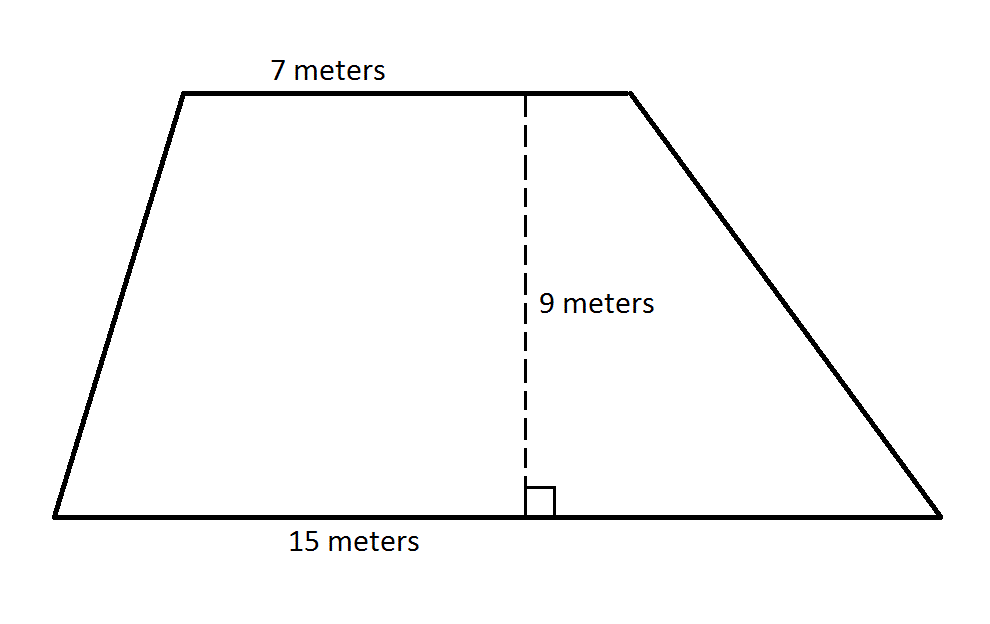
Trapezoid

What is the area of the trapezoid?

Possible Answers:

$198\textrm{ m}^{2}$

$63\textrm{ m}^{2}$

$99\textrm{ m}^{2}$

$135\textrm{ m}^{2}$

$105\textrm{ m}^{2}$

Correct answer:

$99\textrm{ m}^{2}$

Explanation:

To find the area of a trapezoid, multiply the sum of the bases (the parallel sides) by the height (the perpendicular distance between the bases), and then divide by 2.

$A = \frac{1}{2} \cdot (7 + 15) \cdot 9 = \frac{1}{2} \cdot 22 \cdot 9 = 99 \textrm{ m}^2$

Report an Error

Example Question #133 : Quadrilaterals

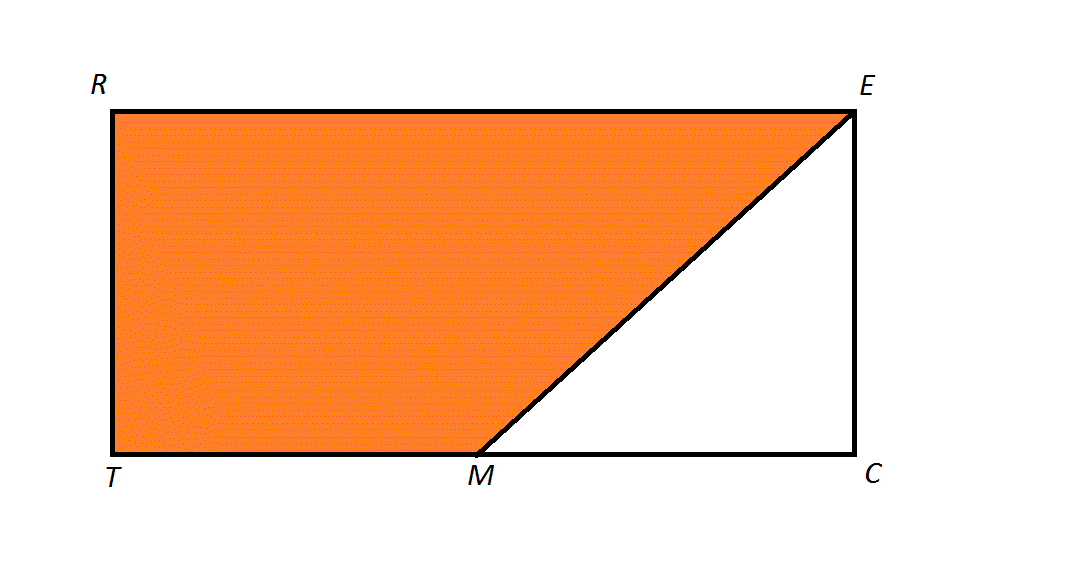
Trapezoid

The above diagram depicts a rectangle RECT with isosceles triangle $\Delta ECM$ . If is the midpoint of $\overline{CT}$ , and the area of the orange region is , then what is the length of one leg of $\Delta ECM$ ?

Possible Answers:

$\sqrt {96}$

$\sqrt {108}$

$\sqrt {48}$

$\sqrt {54}$

Correct answer:

$\sqrt {48}$

Explanation:

The length of a leg of $\Delta ECM$ is equal to the height of the orange region, which is a trapezoid. Call this length/height .

Since the triangle is isosceles, then CM = h , and since is the midpoint of $\overline{CT}$ , MT = h . Also, since opposite sides of a rectangle are congruent,

RE = CT = CM + MT = h + h = 2h

Therefore, the orange region is a trapezoid with bases and and height . Its area is 72, so we can set up and solve this equation using the area formula for a trapezoid:

$\frac{1}{2} (B + b)h = 72$

$\frac{1}{2} (2h + h)h = 72$

$\frac{1}{2} (3h )h = 72$

$\frac{3}{2}h^{2} = 72$

$\frac{3}{2}h^{2} \cdot \frac{2}{3} = 72 \cdot \frac{2}{3}$

$h^{2}= 48$

$h = \sqrt {48}$

This is the length of one leg of the triangle.

Report an Error

Example Question #134 : Quadrilaterals

A trapezoid has a height of inches and bases measuring inches and inches. What is its area?

Possible Answers:

$750\; \textrm{in}^{2}$

$864\; \textrm{in}^{2}$

$1,500\; \textrm{in}^{2}$

$900\; \textrm{in}^{2}$

$600\; \textrm{in}^{2}$

Correct answer:

$750\; \textrm{in}^{2}$

Explanation:

Use the following formula, with B = 36,b = 24,h=25 :

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (36+24) \cdot 25 = 750$

Report an Error

Example Question #4 : How To Find The Area Of A Trapezoid

What is the area of a trapezoid with height 20 inches and bases of length 100 and 200?

Possible Answers:

$2,000\; \textrm{in}^{2}$

$6,000\; \textrm{in}^{2}$

$4,000\; \textrm{in}^{2}$

$1,000\; \textrm{in}^{2}$

$3,000\; \textrm{in}^{2}$

Correct answer:

$3,000\; \textrm{in}^{2}$

Explanation:

Set B=200 , b=100 , h = 20 .

The area of a trapezoid can be found using this formula:

$A = \frac{1}{2} (B+b)h = \frac{1}{2} (200+100) \cdot 20 = 3,000$

The area is 3,000 square inches.

Report an Error

View SSAT- Middle Level Tutors

Jason
Certified Tutor

NJCU, Bachelor in Arts, Communication, General. Saint Peters College, Masters in Business Administration, Elementary and Midd...

View SSAT- Middle Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Middle Level Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in San Francisco-Bay Area, Biology Tutors in Atlanta, Physics Tutors in Phoenix, Spanish Tutors in Seattle, GRE Tutors in Chicago, Calculus Tutors in Atlanta, MCAT Tutors in Seattle, English Tutors in Chicago, English Tutors in Dallas Fort Worth, Math Tutors in Seattle

Popular Courses & Classes

Spanish Courses & Classes in New York City, GRE Courses & Classes in Seattle, SSAT Courses & Classes in San Diego, SSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Phoenix, LSAT Courses & Classes in Boston, GMAT Courses & Classes in Atlanta, SSAT Courses & Classes in New York City, ACT Courses & Classes in Philadelphia, ACT Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in Denver, SAT Test Prep in New York City, ACT Test Prep in New York City, GRE Test Prep in Houston, ISEE Test Prep in Atlanta, GMAT Test Prep in Phoenix, ISEE Test Prep in Denver, MCAT Test Prep in San Diego, ACT Test Prep in Philadelphia, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Trapezoids

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #3 : How To Find The Area Of A Trapezoid

Example Question #3 : How To Find The Area Of A Trapezoid

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #131 : Quadrilaterals

Example Question #132 : Quadrilaterals

Example Question #133 : Quadrilaterals

Example Question #134 : Quadrilaterals

Example Question #4 : How To Find The Area Of A Trapezoid

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: