We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Fractions

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #343 : Fractions

$13\frac{3}{9}+6\frac{4}{9}$ $\displaystyle 13\frac{3}{9}+6\frac{4}{9}$

Possible Answers:

$17\frac{6}{}9$ $\displaystyle 17\frac{6}{}9$

$18\frac{6}{}9$ $\displaystyle 18\frac{6}{}9$

$18\frac{7}{}9$ $\displaystyle 18\frac{7}{}9$

$17\frac{7}{}9$ $\displaystyle 17\frac{7}{}9$

$19\frac{7}{}9$ $\displaystyle 19\frac{7}{}9$

Correct answer:

$19\frac{7}{}9$ $\displaystyle 19\frac{7}{}9$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

13+6=19 $\displaystyle 13+6=19$

$\frac{3}{9}+\frac{4}{9}=\frac{7}{9}$ $\displaystyle \frac{3}{9}+\frac{4}{9}=\frac{7}{9}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #161 : How To Add Fractions

$12\frac{3}{9}+17\frac{2}{9}$ $\displaystyle 12\frac{3}{9}+17\frac{2}{9}$

Possible Answers:

$27\frac{6}{9}$ $\displaystyle 27\frac{6}{9}$

$29\frac{5}{9}$ $\displaystyle 29\frac{5}{9}$

$27\frac{5}{9}$ $\displaystyle 27\frac{5}{9}$

$29\frac{4}{9}$ $\displaystyle 29\frac{4}{9}$

$29\frac{6}{9}$ $\displaystyle 29\frac{6}{9}$

Correct answer:

$29\frac{5}{9}$ $\displaystyle 29\frac{5}{9}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

$\displaystyle 12+17=29$

$\frac{3}{9}+\frac{2}{9}=\frac{5}{9}$ $\displaystyle \frac{3}{9}+\frac{2}{9}=\frac{5}{9}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #344 : Fractions

$17\frac{4}{11}+9\frac{4}{11}$ $\displaystyle 17\frac{4}{11}+9\frac{4}{11}$

Possible Answers:

$26\frac{8}{11}$ $\displaystyle 26\frac{8}{11}$

$26\frac{9}{11}$ $\displaystyle 26\frac{9}{11}$

$27\frac{8}{11}$ $\displaystyle 27\frac{8}{11}$

$27\frac{9}{11}$ $\displaystyle 27\frac{9}{11}$

$25\frac{9}{11}$ $\displaystyle 25\frac{9}{11}$

Correct answer:

$26\frac{8}{11}$ $\displaystyle 26\frac{8}{11}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

17+9=26 $\displaystyle 17+9=26$

$\frac{4}{11}+\frac{4}{11}=\frac{8}{11}$ $\displaystyle \frac{4}{11}+\frac{4}{11}=\frac{8}{11}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #501 : Number & Operations: Fractions

$22\frac{3}{11}+13\frac{6}{11}$ $\displaystyle 22\frac{3}{11}+13\frac{6}{11}$

Possible Answers:

$33\frac{8}{11}$ $\displaystyle 33\frac{8}{11}$

$33\frac{9}{11}$ $\displaystyle 33\frac{9}{11}$

$35\frac{8}{11}$ $\displaystyle 35\frac{8}{11}$

$34\frac{9}{11}$ $\displaystyle 34\frac{9}{11}$

$35\frac{9}{11}$ $\displaystyle 35\frac{9}{11}$

Correct answer:

$35\frac{9}{11}$ $\displaystyle 35\frac{9}{11}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

$\displaystyle 22+13=35$

$\frac{3}{11}+\frac{6}{11}=\frac{9}{11}$ $\displaystyle \frac{3}{11}+\frac{6}{11}=\frac{9}{11}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #502 : Number & Operations: Fractions

$13\frac{5}{13}+5\frac{2}{13}$ $\displaystyle 13\frac{5}{13}+5\frac{2}{13}$

Possible Answers:

$17\frac{7}{13}$ $\displaystyle 17\frac{7}{13}$

$19\frac{8}{13}$ $\displaystyle 19\frac{8}{13}$

$18\frac{7}{13}$ $\displaystyle 18\frac{7}{13}$

$18\frac{8}{13}$ $\displaystyle 18\frac{8}{13}$

$19\frac{7}{13}$ $\displaystyle 19\frac{7}{13}$

Correct answer:

$18\frac{7}{13}$ $\displaystyle 18\frac{7}{13}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

13+5=18 $\displaystyle 13+5=18$

$\frac{5}{13}+\frac{2}{13}=\frac{7}{13}$ $\displaystyle \frac{5}{13}+\frac{2}{13}=\frac{7}{13}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #503 : Number & Operations: Fractions

$38\frac{6}{12}+12\frac{1}{12}$ $\displaystyle 38\frac{6}{12}+12\frac{1}{12}$

Possible Answers:

$50\frac{7}{12}$ $\displaystyle 50\frac{7}{12}$

$50\frac{9}{12}$ $\displaystyle 50\frac{9}{12}$

$52\frac{7}{12}$ $\displaystyle 52\frac{7}{12}$

$50\frac{8}{12}$ $\displaystyle 50\frac{8}{12}$

$52\frac{8}{12}$ $\displaystyle 52\frac{8}{12}$

Correct answer:

$50\frac{7}{12}$ $\displaystyle 50\frac{7}{12}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

$\displaystyle 38+12=50$

$\frac{6}{12}+\frac{1}{12}=\frac{7}{12}$ $\displaystyle \frac{6}{12}+\frac{1}{12}=\frac{7}{12}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #511 : Number & Operations: Fractions

$13\frac{1}{5}+14\frac{2}{5}$ $\displaystyle 13\frac{1}{5}+14\frac{2}{5}$

Possible Answers:

$28\frac{3}{5}$ $\displaystyle 28\frac{3}{5}$

$27\frac{3}{5}$ $\displaystyle 27\frac{3}{5}$

$29\frac{1}{5}$ $\displaystyle 29\frac{1}{5}$

$29\frac{2}{5}$ $\displaystyle 29\frac{2}{5}$

$26\frac{3}{5}$ $\displaystyle 26\frac{3}{5}$

Correct answer:

$27\frac{3}{5}$ $\displaystyle 27\frac{3}{5}$

Explanation:

When we add mixed numbers, we add whole numbers to whole numbers and fractions to fractions.

$\displaystyle 13+14=27$

$\frac{1}{5}+\frac{2}{5}=\frac{3}{5}$ $\displaystyle \frac{1}{5}+\frac{2}{5}=\frac{3}{5}$

Remember, when we are adding fractions we must have common denominators and we only add the numerators.

Report an Error

Example Question #1241 : Common Core Math: Grade 4

Select the fraction model that shows the sum of $\frac{1}{8}+\frac{1}{8}$ $\displaystyle \frac{1}{8}+\frac{1}{8}$

Possible Answers:

4 8

2 6

3 8

5 8

2 8

Correct answer:

2 8

Explanation:

$\frac{1}{8}+\frac{1}{8}=\frac{2}{8}$ $\displaystyle \frac{1}{8}+\frac{1}{8}=\frac{2}{8}$

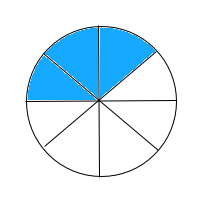
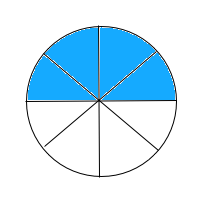
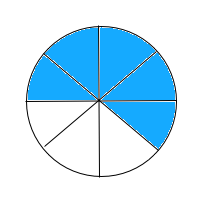
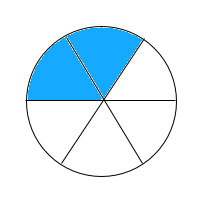
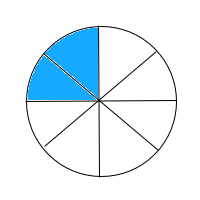
The fraction model is broken up into eight pieces and two of the pieces are shaded in. The numerator of the fraction tells us how many pieces should be shaded in, and the denominator tells us how many pieces the whole should be split up into.

Report an Error

Example Question #2 : Adding Fractions In Word Problems

In Stuart's pantry, $\frac{1}{5}$ $\displaystyle \frac{1}{5}$ of the items are chips and $\frac{1}{5}$ $\displaystyle \frac{1}{5}$ of the items are cereal. What fraction of the items are chips or cereal?

Possible Answers:

$\frac{1}{5}$ $\displaystyle \frac{1}{5}$

$\frac{2}{5}$ $\displaystyle \frac{2}{5}$

$\frac{5}{5}$ $\displaystyle \frac{5}{5}$

$\frac{4}{5}$ $\displaystyle \frac{4}{5}$

$\frac{3}{5}$ $\displaystyle \frac{3}{5}$

Correct answer:

$\frac{2}{5}$ $\displaystyle \frac{2}{5}$

Explanation:

To solve this problem, we are putting the chips and the cereal together, so we add the fractions.

$\frac{1}{5}+\frac{1}{5}=\frac{2}{5}$ $\displaystyle \frac{1}{5}+\frac{1}{5}=\frac{2}{5}$

2 5

Report an Error

Example Question #1 : Adding Fractions In Word Problems

In Andy's pantry, $\frac{3}{5}$ $\displaystyle \frac{3}{5}$ of the items are chips and $\frac{1}{5}$ $\displaystyle \frac{1}{5}$ of the items are cereal. What fraction of the items are chips or cereal?

Possible Answers:

$\frac{4}{5}$ $\displaystyle \frac{4}{5}$

$\frac{2}{5}$ $\displaystyle \frac{2}{5}$

$\frac{1}{5}$ $\displaystyle \frac{1}{5}$

$\frac{5}{5}$ $\displaystyle \frac{5}{5}$

$\frac{3}{5}$ $\displaystyle \frac{3}{5}$

Correct answer:

$\frac{4}{5}$ $\displaystyle \frac{4}{5}$

Explanation:

To solve this problem, we are putting the chips and the cereal together, so we add the fractions.

$\frac{3}{5}+\frac{1}{5}=\frac{4}{5}$ $\displaystyle \frac{3}{5}+\frac{1}{5}=\frac{4}{5}$

4 5

Report an Error

View SSAT- Middle Level Tutors

Lindsey
Certified Tutor

California State University-Fresno, Bachelor of Science, Ecology and Evolutionary Biology. National University, Certificate, ...

View SSAT- Middle Level Tutors

Iffy
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Computer Engineering, General. University of Maryland-College P...

View SSAT- Middle Level Tutors

Maggie
Certified Tutor

New York University, Bachelor of Science, Digital Communications and Multimedia.

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Los Angeles, MCAT Tutors in Philadelphia, Spanish Tutors in Chicago, Algebra Tutors in Dallas Fort Worth, ACT Tutors in Boston, French Tutors in Chicago, Calculus Tutors in Houston, LSAT Tutors in New York City, Biology Tutors in Dallas Fort Worth, Computer Science Tutors in Houston

Popular Courses & Classes

SAT Courses & Classes in Phoenix, SAT Courses & Classes in San Diego, ACT Courses & Classes in Boston, SAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Los Angeles, Spanish Courses & Classes in Philadelphia, MCAT Courses & Classes in Los Angeles, GRE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Houston, GMAT Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in Phoenix, GRE Test Prep in Los Angeles, ISEE Test Prep in Atlanta, ISEE Test Prep in Seattle, ISEE Test Prep in Phoenix, ACT Test Prep in Boston, SAT Test Prep in Phoenix, GRE Test Prep in Houston, GMAT Test Prep in Denver, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Fractions

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #343 : Fractions

Example Question #161 : How To Add Fractions

Example Question #344 : Fractions

Example Question #501 : Number & Operations: Fractions

Example Question #502 : Number & Operations: Fractions

Example Question #503 : Number & Operations: Fractions

Example Question #511 : Number & Operations: Fractions

Example Question #1241 : Common Core Math: Grade 4

Example Question #2 : Adding Fractions In Word Problems

Example Question #1 : Adding Fractions In Word Problems

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Fractions

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #343 : Fractions

Example Question #161 : How To Add Fractions

Example Question #344 : Fractions

Example Question #501 : Number & Operations: Fractions

Example Question #502 : Number & Operations: Fractions

Example Question #503 : Number & Operations: Fractions

Example Question #511 : Number & Operations: Fractions

Example Question #1241 : Common Core Math: Grade 4

Example Question #2 : Adding Fractions In Word Problems

Example Question #1 : Adding Fractions In Word Problems

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Example Question #501 : Number & Operations: Fractions

Example Question #502 : Number & Operations: Fractions

Example Question #503 : Number & Operations: Fractions

Example Question #511 : Number & Operations: Fractions