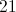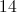SSAT Middle Level Math : How to find the part from the whole
Study concepts, example questions & explanations for SSAT Middle Level Math
All SSAT Middle Level Math Resources
Example Questions
Example Question #1 : How To Find The Part From The Whole
It took Julia 15 minutes to walk 1 mile. If she walks for 2 more miles at the same speed, what part of an hour will her entire 3-mile walk take?
It will take her 30 more minutes to finish her walk for a total of 45 minutes. 45 minutes of 60 minutes in an hour is the same as 
Example Question #1022 : Ssat Middle Level Quantitative (Math)
The sum of the factors of 12 is
The factors of 12 are 1, 12, 3, 4, 2, and 6. The sum of them is when you add all of them together. 
Example Question #1023 : Ssat Middle Level Quantitative (Math)
There are 
If 
If this is true, then 
Example Question #2 : How To Find The Part From The Whole
The ratio of women to men in a meeting with 56 people is 5 to 3. How many more women then men are there?
The best way to think about this problem is to divide the total number of people into parts. Since there are 5 parts women to 3 parts men, it's best to divide the total into 8 parts. Dividing 56 into 8 parts gives you 7. 7 is your multiplier. Now take your multiplier (7) and multiply it by your ratios.
This give you 
The difference between 35 and 21 is 14.
Example Question #3 : How To Find The Part From The Whole
Robert's dog is 4 years older than Karen's cat. In 3 years, the sum of the ages of Robert's dog and Karen's cat will be 13. How old is Robert's dog right now?
We can solve this problem by backsolving, meaning plugging in the answer choices.
If we plug in 7 for the dog's age, that means that in 3 years, the dog will be 10.
That also means that the cat is 3 since the dog is 4 years older.
The sum of 10 and 3 is 13, so the answer choice of 7 is the correct answer.
Example Question #4 : How To Find The Part From The Whole
There are 
If 
Now we can write the following proportion and solve.
Example Question #5 : How To Find The Part From The Whole
The ratio of doctors to nurses in the hospital with a staff of 
The best way to think about this problem is to divide the total number of people into parts. Since there are 
This gives you 
To find how many more nurses than doctors there are we take the difference:
Therefore, there are 
Example Question #1034 : Ssat Middle Level Quantitative (Math)
Alice received $2.40 for her weekly allowance. If her favorite snacks cost 60¢ each, how many snacks can Alice buy this week?
To solve:
Divide the total amount of Alice's allowance ($2.40) by the price for each snack ($ .60)
Alice would be able to buy 4 snacks.
Example Question #1034 : Ssat Middle Level Quantitative (Math)
Steve ate 20% of his pie on Monday. On Tuesday Steve ate 50% of the left-over pie. What percent of the pie is left?
10%
40%
30%
20%
60%
40%
On Tuesday, Steve ate 50% (half) of the 80%, which is 40%. Steve has eaten 20% on Monday and 40% on Tuesday, so there is 40% left over.
Example Question #1035 : Ssat Middle Level Quantitative (Math)
As a swim team member, Nicolas needs to train 90 hours a month. How many hours should Nicolas train each day of the 30-day month, in order to reach his goal?
Divide 90 hours by 30 days in the month:
Answer: Nicolas needs to train 3 hours a day.
Certified Tutor
All SSAT Middle Level Math Resources
