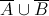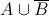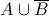Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Data Analysis and Probability

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #644 : Ssat Middle Level Quantitative (Math)

Vt_custome_venn_diagram_series_

The above Venn diagram shows the amount of survey respondents that only like tacos, only like tamales, and those that like both tacos and tamales.

What fraction of respondents like both tacos and tamales?

Possible Answers:

$\frac{4}{10}$

$\frac{1}{10}$

$\frac{2}{5}$

$\frac{1}{5}$

Correct answer:

$\frac{1}{5}$

Explanation:

The total number of survey respondents is equal to 100 percent, which equals $\frac{5}{5}$ .

The total number of respondents that do not like both tacos and tamales: $\frac{3}{5}+\frac{1}{5}=\frac{4}{5}$ .

The remaining amount equals the respondents that like both tacos and tamales.

Thus, the solution is:

$\frac{5}{5}-\frac{4}{5}=\frac{1}{5}$

Report an Error

Example Question #645 : Ssat Middle Level Quantitative (Math)

Vt_custome_venn_diagram_series_

The above Venn diagram shows the amount of survey respondents that only like tacos, only like tamales, and those that like both tacos and tamales.

What percent of the respondents like both tamales and tacos?

Possible Answers:

$5\%$

$1\%$

$20\%$

$25\%$

Correct answer:

$20\%$

Explanation:

The remaining amount equals the respondents that like both tacos and tamales.

Thus, the solution is:

$\frac{5}{5}-\frac{4}{5}=\frac{1}{5}$

Now we need to convert the fraction into a percent.

$\frac{1}{5}=\frac{1}{5}\times \frac{20}{20}=\frac{20}{100}=20\%$

Report an Error

Example Question #646 : Ssat Middle Level Quantitative (Math)

Vt_custome_venn_diagram_series_

The above Venn diagram shows the results from a recent survey. Respondents had the choice of being only a fan of TEAM , only a fan of TEAM , or a fan of both of the teams. What percentage of the respondents are fans of both the teams?

Possible Answers:

$23\%$

$21\%$

$26\%$

$33\%$

Correct answer:

$23\%$

Explanation:

In order to find the value of the common area of this Venn diagram, find the sum of percent and percent.

Then find the difference from the sum to 100 percent.

The solution is:

56+21=77

100-77=23

Report an Error

Example Question #1 : How To Use A Venn Diagram

Venn_diagram

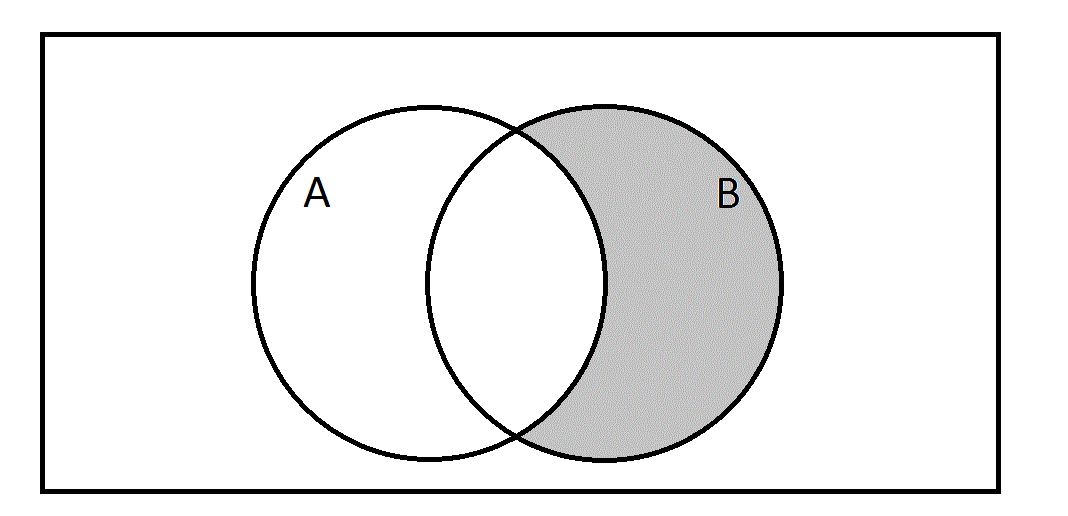
See the above Venn diagram. Which of the following sets is represented by the gray region?

Possible Answers:

$\overline{A} \cup \overline{B}$

$A \cap \overline{B}$

$\overline{A} \cup B$

$\overline{A} \cap B$

$A \cup \overline{B}$

Correct answer:

$\overline{A} \cap B$

Explanation:

The shaded area represents the set of all elements that are both in and not in . This the intersection of and the complement of , or $\overline{A} \cap B$ .

Report an Error

Example Question #1 : How To Use A Venn Diagram

Venn_diagram_2

See the above Venn diagram. Which of the following sets is represented by the gray region?

Possible Answers:

$\overline{A }\cap \overline{B}$

$\overline{A }\cap B$

$\overline{A }\cup \overline{B}$

$A \cup \overline{B}$

$\overline{A }\cup B$

Correct answer:

$A \cup \overline{B}$

Explanation:

The gray region represents all elements that either are in , are not in - that is, are in $\overline{B}$ - or both. This is the union of and $\overline{B}$ , or $A \cup \overline{B}$ .

Report an Error

Example Question #1 : Venn Diagrams

Given the Venn diagram below, which of the following does not belong to $A \cup B$ ?

Possible Answers:

Correct answer:

Explanation:

The symbol $\cup$ stands for the union between two sets. Therefore, $A\cup B$ means the set of all numbers that are in either A or B. Looking at our choices, the only number that isn't in either A, B, or both is 23.

Report an Error

Example Question #1 : Data Analysis

Venn_4

Let set $U = \mathbb{N}$ , the set of all natural numbers.

= { | is a multiple of 6 }

= { | is a multiple of 9 }

Which of the following numbers would appear in the gray region of the Venn diagram?

Possible Answers:

8,544

4,572

4,077

3,438

9,349

Correct answer:

4,077

Explanation:

The gray area represents the portion of that is not in - in other words, all multiples of 9 that are not also multiples of 6.

$4,572 \div 6 = 762$

$3,438 \div 6 = 573$

$8,544 \div 6 =1,424$

Therefore, 4,572, 3,438, and 8,544 can be eliminated.

$9,349 \div 9 = 1,038 \;R\; 7$ , so 9,349 can be eliminated because it isn't a multiple of 9.

$4,077 \div 6 = 679 \; R \; 3$ and $4,077 \div 9 = 453$ , so, as both a nonmultiple of 6 and a multiple of 9, 4.077 is the correct choice.

Report an Error

Example Question #2 : How To Use A Venn Diagram

Vt custom venn series ssat middle

The above Venn diagram represents survey respondents from a recent political poll. Based on the respondent's political affiliation, they were classified into group only, only or both groups.

What percentage of the respondents were classified into both groups?

Possible Answers:

$62\%$

$60\%$

$29\%$

$78\%$

$26\%$

Correct answer:

$29\%$

Explanation:

The common portion of this Venn diagram represents the percentage of respondents that were classified into both groups. In order to calculate the percentage that represents the amount of respondents classified into both groups, first find the sum of group and group . Then subtract that quantity from 100 percent.

The solution is:

62+9=71

100-71=29

Report an Error

Example Question #1 : How To Use A Venn Diagram

Vt custom venn series ssat middle

Mr. Robinson surveyed his class to find out what his students planned on doing during their summer vacation. Every student in his class stated that they planned on swimming with their friends and/or travel with their family.

What percentage of Mr. Robinson’s class planned on both swimming with their friends and traveling with their family?

Possible Answers:

$56\%$

$23\%$

$77\%$

$46\%$

$54\%$

Correct answer:

$23\%$

Explanation:

The common portion of this Venn diagram represents the percentage of Mr. Robinson's students that stated they planned on both swimming and traveling during the summer. In order to calculate the percentage that represents the amount of students classified into both groups, first find the sum of the swimming group and traveling group. Then subtract that sum from $100\%$ .

The solution is:

54+23=77

100-77=23

Report an Error

Example Question #6 : How To Use A Venn Diagram

Vt custom venn series ssat middle

Kelly and Antonio are in a group together on a popular social media website. They realized that within the group they have mutual friendships as well as friendships exclusive of one another.

What ratio accurately represents the amount of friendships within the group that they have in common to those that they do not have in common?

Possible Answers:

2:5

3:4

6:20

10:60

1:4

Correct answer:

2:5

Explanation:

In order to find the ratio of friends that Kelly and Antonio have in common compared to the group members who are only friends with one or the other first find the percentage value of the common portion of the Venn diagram. To calculate this value, find the sum of the two exclusive groups and then subtract that sum from $100\%$ .

27+33=60

100-60=40

This means that $40\%$ of the group members are common friends of Kelly and Antonio. To convert this percentage to a ratio, first write $40\%$ as a fraction, and then simplify as a ratio.

$40\%$ is equal to: $\frac{40}{100}=40:100=4:10=2:5$

This means that out of every group members are mutual friends of Kelly and Antonio.

Report an Error

View SSAT- Middle Level Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

View SSAT- Middle Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SSAT- Middle Level Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Denver, Statistics Tutors in Denver, ISEE Tutors in Phoenix, GRE Tutors in Chicago, GRE Tutors in Miami, ISEE Tutors in Dallas Fort Worth, ACT Tutors in Boston, Biology Tutors in Atlanta, Spanish Tutors in Atlanta, ISEE Tutors in Atlanta

Popular Courses & Classes

ISEE Courses & Classes in San Diego, LSAT Courses & Classes in Atlanta, LSAT Courses & Classes in Miami, MCAT Courses & Classes in Atlanta, GRE Courses & Classes in Miami, MCAT Courses & Classes in Houston, Spanish Courses & Classes in Atlanta, GMAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Denver, LSAT Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Chicago, GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Phoenix, SSAT Test Prep in Seattle, LSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Seattle, GRE Test Prep in Denver, ISEE Test Prep in Atlanta, SSAT Test Prep in Washington DC, GRE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Data Analysis and Probability

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #644 : Ssat Middle Level Quantitative (Math)

Example Question #645 : Ssat Middle Level Quantitative (Math)

Example Question #646 : Ssat Middle Level Quantitative (Math)

Example Question #1 : How To Use A Venn Diagram

Example Question #1 : How To Use A Venn Diagram

Example Question #1 : Venn Diagrams

Example Question #1 : Data Analysis

Example Question #2 : How To Use A Venn Diagram

Example Question #1 : How To Use A Venn Diagram

Example Question #6 : How To Use A Venn Diagram

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: