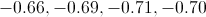Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Elementary Level Math : Sets

Study concepts, example questions & explanations for SSAT Elementary Level Math

Create An Account

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Measurement & Data

Which would make the most sense to use if we were going to measure a candle?

Possible Answers:

Measuring tape

Yardstick

Meter stick

Ruler

Correct answer:

Ruler

Explanation:

You would use a ruler to measure a shoe because a candle is most likely smaller than 12 inches, which is the size of a ruler. All of the other tools will be much larger.

Report an Error

Example Question #1 : Measurement & Data

Which would make the most sense to use if we were going to measure a taco?

Possible Answers:

Measuring tape

Meter stick

Yardstick

Ruler

Correct answer:

Ruler

Explanation:

You would use a ruler to measure a taco because a taco is most likely smaller than 12 inches, which is the size of a ruler. All of the other tools will be much larger.

Report an Error

Example Question #1 : How To Identify The Parts Of A List

$Place\;the\;following\;numbers\;in\;order\;from\;least\;to\;greatest: -3,\frac{1}{2},0,-50$

Possible Answers:

$0,\frac{1}{2},-50,-3$

$\frac{1}{2},0,-3,-50$

$-50,-3,0,\frac{1}{2}$

$-50,-3,\frac{1}{2},0$

Correct answer:

$-50,-3,0,\frac{1}{2}$

Explanation:

$-50< -3< 0< \frac{1}{2}$

$Negative\;numbers\;are\;smaller\;than\;0.$

$Positive\;number\;are\;greater\;than\;0.$

Report an Error

Example Question #2 : How To Identify The Parts Of A List

Which of the choices below lists ONLY examples of triangles?

Possible Answers:

equilateral, parallelogram, trapezoid

rhombus, kite, trapezoid

isosceles, scalene, equilateral

pentagon, isosceles, kite

Correct answer:

isosceles, scalene, equilateral

Explanation:

isosceles: triangle with two equal sides and two equal angles

scalene: triangle with no equal sides and no equal angles

equilateral: triangle with three equal sides and three equal angles

Report an Error

Example Question #4901 : Ssat Elementary Level Quantitative (Math)

Define the set $C = \left \{ 2, 4, 6, 8, 10, 12, 14, 16, 18, 20\right \}$

Which of the following is a subset of ?

Possible Answers:

$\left \{ 1, 4, 8, 12, 20\right \}$

$\left \{ 4, 8, 12, 16, 20\right \}$

$\left \{ 4, 6, 8, 10, 11, 14\right \}$

$\left \{ 8, 9, 10, 12, 16, 18\right \}$

$\left \{ 2, 4, 6, 9, 12, 14\right \}$

Correct answer:

$\left \{ 4, 8, 12, 16, 20\right \}$

Explanation:

A subset of a set , by definition, is any set that contains no elements not in . Each of the following subsets can be seen to have at least one such element, which is underlined here:

$\left \{ \underline{1}, 4, 8, 12, 20\right \}$

$\left \{ 8, \underline{9}, 10, 12, 16, 18\right \}$

$\left \{ 4, 6, 8, 10,\underline{ 11}, 14\right \}$

$\left \{ 2, 4, 6, \underline{9}, 12, 14\right \}$

The remaining set can be seen to have only elements from :

$\left \{ 4, 8, 12, 16, 20\right \}\subseteq \left \{ 2, \underline{4}, 6, \underline{8}, 10, \underline{12}, 14, \underline{16}, 18, \underline{20}\right \}$

This is the correct choice.

Report an Error

Example Question #4902 : Ssat Elementary Level Quantitative (Math)

Define two sets as follows:

$A = \left \{ a, b, d, f, h, i, j \right \}$

$B = \left \{ b, c, d, e, h, k, m, p\right \}$

How many elements are in $A \cup B$ ?

Possible Answers:

Correct answer:

Explanation:

$A \cup B$ is the union of sets and - the set of all elements that appear in either or . These elements are:

$\left \{ a, b,c, d,e, f, h, i, j,k,m,p \right \}$

which is a set with twelve elements.

Report an Error

Example Question #2 : How To Identify The Parts Of A List

$17 \times11=187$

$22\times11=242$

$36\times11=396$

$45\times11=495$

$53\times11=583$

$62\times11=682$

Use the given multiplication to find a pattern, and then solve the following:

$a)\;23\times11$

$b)\;72\times11$

$c)\:44 \times11$

Possible Answers:

$a)\:253$

$b)\;792$

$c)\:484$

$a)\:412$

$b)\;827$

$c)\:399$

$a)\ 444$

$b)\ 888$

$c)\ 311$

$a)\:293$

$b)\;732$

$c)\:464$

$a)\:341$

$b)\;741$

$c)\:311$

Correct answer:

$a)\:253$

$b)\;792$

$c)\:484$

Explanation:

$When\: multiplying \: numbers \: by \: 11, \: the \: sum \: goes \: in\: between \: the \: two \: digits.$

$43\times11=4\underline{7}3\Rightarrow 4\;\underline{4+3} \;3$

$15\times11=1\underline{6}5\Rightarrow 1\;\underline{1+5} \;5$

Report an Error

Example Question #3 : How To Identify The Parts Of A List

Place the following numbers in order from smallest to largest: -0.71,-0.69,-0.70,-0.66

Possible Answers:

-0.69,-0.66,-0.70,-0.71

-0.66,-0.69,-0.71,-0.70

-0.71,-0.69,-0.70,-0.66

-0.71,-0.70,-0.69,-0.66

-0.66,-0.69,-0.70,-0.71

Correct answer:

-0.71,-0.70,-0.69,-0.66

Explanation:

For negative numbers, the bigger the value next to the negative sign, the smaller the number. For example, is smaller than .

Use the tenths digit (the one to the right of the decimal point) to order the numbers:

The negative numbers with a in the tenths place are smaller than the numbers with a in the tenths place.

Then, use the hundredths place to order the numbers:

-0.69 is smaller than -0.66 since is larger than .

-0.71 is smaller than -0.70 since is larger than .

Report an Error

Example Question #3 : How To Identify The Parts Of A List

Which of these numbers is not a prime number?

Possible Answers:

Correct answer:

Explanation:

A prime number has exactly two factors: 1 and itself. 85 is immediately disqualified: any number that ends in 5 has 5 as a factor.

Report an Error

Example Question #4 : How To Identify The Parts Of A List

Place the following numbers in order from least to greatest: 0.71,0.69,0.70,0.66

Possible Answers:

0.66,0.69,0.70,0.71

0.69,0.66,0.70,0.71

0.66,0.69,0.71,0.70

0.71,0.70,0.69,0.66

Correct answer:

0.66,0.69,0.70,0.71

Explanation:

First, use the tenths digit (the one to the right of the decimal point) to order the numbers.

The numbers with a 6 in the tenths place are smaller than the numbers with a 7 in the tenths place.

Then, use the hundredths place to order the numbers.

0.66 is smaller than 0.69 since 6 is smaller than 9.

0.70 is smaller than 0.71 since 0 is smaller than 1.

Report an Error

View SSAT- Elementary Level Tutors

Altagrace
Certified Tutor

Florida International University, Bachelors, Communication and Psychology.

View SSAT- Elementary Level Tutors

Rima
Certified Tutor

Lebanese university , Master's/Graduate, Marketing and Management .

View SSAT- Elementary Level Tutors

Kaitlyn
Certified Tutor

Fairfield University, Bachelor of Science, Biology, General. NUI Galway Ireland, Master of Science, Neuroscience.

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in New York City, Chemistry Tutors in Boston, MCAT Tutors in Los Angeles, Algebra Tutors in Chicago, Calculus Tutors in Los Angeles, Algebra Tutors in New York City, Calculus Tutors in Washington DC, English Tutors in Boston, Biology Tutors in San Diego, Spanish Tutors in Philadelphia

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Boston, SAT Courses & Classes in Phoenix, GRE Courses & Classes in Atlanta, MCAT Courses & Classes in Denver, ISEE Courses & Classes in New York City, SSAT Courses & Classes in Washington DC, LSAT Courses & Classes in Chicago, LSAT Courses & Classes in Phoenix, SSAT Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Phoenix, SAT Test Prep in Denver, ISEE Test Prep in New York City, MCAT Test Prep in San Diego, ACT Test Prep in Miami, MCAT Test Prep in New York City, GMAT Test Prep in Washington DC, ACT Test Prep in San Diego, SSAT Test Prep in Boston, SSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Elementary Level Math : Sets

Study concepts, example questions & explanations for SSAT Elementary Level Math

All SSAT Elementary Level Math Resources

Example Questions

Example Question #1 : Measurement & Data

Example Question #1 : Measurement & Data

Example Question #1 : How To Identify The Parts Of A List

Example Question #2 : How To Identify The Parts Of A List

Example Question #4901 : Ssat Elementary Level Quantitative (Math)

Example Question #4902 : Ssat Elementary Level Quantitative (Math)

Example Question #2 : How To Identify The Parts Of A List

Example Question #3 : How To Identify The Parts Of A List

Example Question #3 : How To Identify The Parts Of A List

Example Question #4 : How To Identify The Parts Of A List

All SSAT Elementary Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: